Integral hyperbolic sine
From Encyclopedia of Mathematics
The special function defined, for real  , by
, by
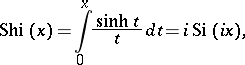 |
where  is the integral sine. The integral hyperbolic sine can be represented by the series
is the integral sine. The integral hyperbolic sine can be represented by the series
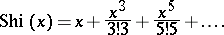 |
It is related to the integral hyperbolic cosine  by
by
 |
where  is the integral logarithm.
is the integral logarithm.
Sometimes it is denoted by  .
.
For references see Integral cosine.
Comments
This function, which is seldom used because of its relation with the sine integral, is also called the hyperbolic sine integral. It can, of course, be defined (as above) for  .
.
How to Cite This Entry:
Integral hyperbolic sine. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Integral_hyperbolic_sine&oldid=11472
Integral hyperbolic sine. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Integral_hyperbolic_sine&oldid=11472
This article was adapted from an original article by A.B. Ivanov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article