Information, transmission rate of
A quantity characterizing the amount of information that is contained in the output signal of a communication channel relative to the input signal, calculated in a unit of time (cf. Information, amount of). If
 |
are stochastic processes in discrete or continuous time, being the input and output signals of a communication channel, then the quantity
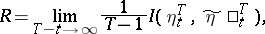 | (*) |
is the transmission rate of information (if the limit exists). Here  is the amount of information,
is the amount of information,  is the segment
is the segment  of
of  and
and  is analogously defined. The existence of the limit in (*) has been proved for the large class of channels in which the signals
is analogously defined. The existence of the limit in (*) has been proved for the large class of channels in which the signals  and
and  are stationary and stationarily-related stochastic processes. An explicit computation of the transmission rate of information is possible, in particular, for a memoryless channel and a Gaussian channel. E.g., for a Gaussian channel, whose signals
are stationary and stationarily-related stochastic processes. An explicit computation of the transmission rate of information is possible, in particular, for a memoryless channel and a Gaussian channel. E.g., for a Gaussian channel, whose signals 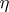 and
and  are Gaussian stationary processes forming a joint Gaussian stationary pair of processes, the transmission rate of information is given by
are Gaussian stationary processes forming a joint Gaussian stationary pair of processes, the transmission rate of information is given by
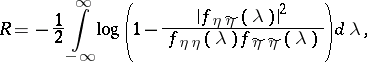 |
where 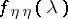 and
and 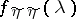 are the spectral densities of
are the spectral densities of  and
and 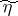 , respectively, and
, respectively, and 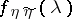 is their joint spectral density.
is their joint spectral density.
References
| [1] | R. Gallagher, "Information theory and reliable communication" , Wiley (1968) |
| [2] | M.S. Pinsker, "Information and informational stability of random variables and processes" , Holden-Day (1964) (Translated from Russian) |
Information, transmission rate of. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Information,_transmission_rate_of&oldid=13228