Index formulas
Relations between analytic and topological invariants of operators of a certain class. More precisely, index formulas establish a relation between the analytic index of a linear operator
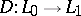 |
(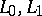 are topological vector spaces), defined by the formula
are topological vector spaces), defined by the formula
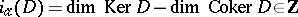 |
and measuring in this way the "difference" between the defective subspaces of 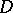 (namely, the kernel
(namely, the kernel 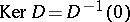 and its cokernel
and its cokernel 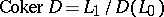 ), and a topological index, namely some topological characteristic of the operator
), and a topological index, namely some topological characteristic of the operator 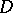 and the spaces
and the spaces 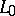 ,
, 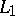 . For a general elliptic differential operator on a closed manifold, the problem of finding index formulas was posed towards the end of the 1950's [1] and solved in 1963 (see [2]), although special forms of index formulas were known even earlier, for example, the Gauss–Bonnet theorem and its multi-dimensional variants. Subsequently a number of generalizations of index formulas were obtained for objects of a more complex nature; in these cases, instead of the index, which is an integer, arbitrary complex numbers and more general objects (e.g. functions) may feature.
. For a general elliptic differential operator on a closed manifold, the problem of finding index formulas was posed towards the end of the 1950's [1] and solved in 1963 (see [2]), although special forms of index formulas were known even earlier, for example, the Gauss–Bonnet theorem and its multi-dimensional variants. Subsequently a number of generalizations of index formulas were obtained for objects of a more complex nature; in these cases, instead of the index, which is an integer, arbitrary complex numbers and more general objects (e.g. functions) may feature.
Elementary index formulas.
1) Let 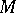 be the differentiable boundary of a bounded region
be the differentiable boundary of a bounded region 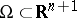 and let
and let 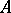 be an elliptic pseudo-differential operator mapping the space
be an elliptic pseudo-differential operator mapping the space 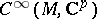 of differentiable complex-valued vector functions on
of differentiable complex-valued vector functions on 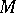 with values in
with values in 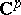 into itself. Let
into itself. Let 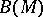 be the manifold of tangent vectors to
be the manifold of tangent vectors to 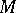 of length
of length 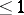 , oriented by means of the
, oriented by means of the 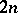 -form
-form
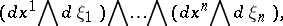 |
where  are local coordinates on
are local coordinates on 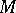 ,
, 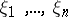 are the corresponding coordinates in the tangent space, and let
are the corresponding coordinates in the tangent space, and let 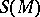 be the oriented boundary of
be the oriented boundary of 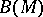 formed by the unit tangent vectors. Since
formed by the unit tangent vectors. Since 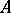 is elliptic, its symbol
is elliptic, its symbol  is a non-singular
is a non-singular 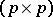 -matrix function on
-matrix function on 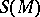 . It turns out that the following Dynin–Fedosov formula holds for the index of
. It turns out that the following Dynin–Fedosov formula holds for the index of 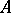 [7]:
[7]:
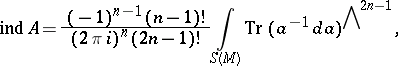 | (1) |
where 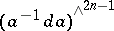 is the exterior power of the matrix exterior form
is the exterior power of the matrix exterior form 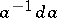 and
and 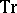 denotes the trace of the
denotes the trace of the 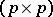 -matrix form. In particular, if
-matrix form. In particular, if 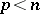 or if
or if 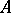 is a differential operator on an odd-dimensional manifold, then
is a differential operator on an odd-dimensional manifold, then 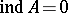 (this is not true, in general, for a pseudo-differential operator).
(this is not true, in general, for a pseudo-differential operator).
2) Let 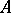 be an elliptic differential operator of the form
be an elliptic differential operator of the form
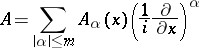 |
(where 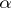 is a multi-index) in the space
is a multi-index) in the space 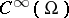 , and let
, and let 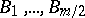 be boundary differential operators from
be boundary differential operators from 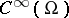 into
into 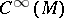 of the form
of the form
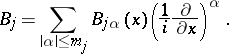 |
The family of operators 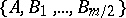 defines an elliptic boundary value problem if the function
defines an elliptic boundary value problem if the function 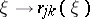 is non-singular on
is non-singular on 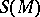 . Here
. Here 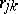 are the coefficients of the polynomials
are the coefficients of the polynomials
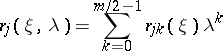 |
that are the remainders after division of the polynomials 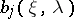 (in
(in 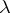 ) by the polynomial
) by the polynomial 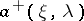 (in
(in 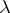 ), where
), where
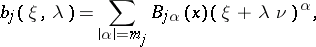 |
and 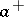 is defined from the factorization
is defined from the factorization 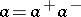 , where
, where
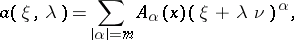 |
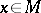 ;
; 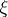 ,
,  are, respectively, a unit tangent vector and the inward normal to
are, respectively, a unit tangent vector and the inward normal to 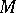 ;
; 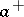 (or
(or 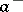 ) is a polynomial (in
) is a polynomial (in 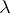 ) without zeros in the upper (respectively, lower)
) without zeros in the upper (respectively, lower) 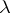 -half-plane. By the index of the above-described boundary value problem one means the index of the corresponding linear operator
-half-plane. By the index of the above-described boundary value problem one means the index of the corresponding linear operator 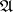 from
from 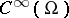 into
into 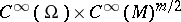 taking
taking 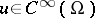 into the set
into the set 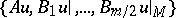 . It turns out that the index of the elliptic boundary value problem is the same as that of the elliptic pseudo-differential operator on
. It turns out that the index of the elliptic boundary value problem is the same as that of the elliptic pseudo-differential operator on 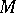 whose symbol is given by the matrix
whose symbol is given by the matrix 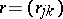 . In particular, the index of the Dirichlet problem
. In particular, the index of the Dirichlet problem 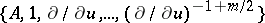 is zero. There are general index formulas for boundary value problems [16], , [27].
is zero. There are general index formulas for boundary value problems [16], , [27].
The Atiyah–Singer index formulas.
Let 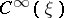 and
and 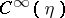 be the spaces of infinitely-differentiable sections of the vector bundles
be the spaces of infinitely-differentiable sections of the vector bundles 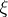 and
and 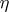 over a closed
over a closed  -dimensional differentiable manifold
-dimensional differentiable manifold 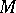 , and let
, and let 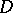 be a (pseudo-differential) elliptic operator acting from
be a (pseudo-differential) elliptic operator acting from 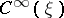 into
into 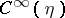 . The topological index
. The topological index 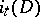 of
of 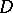 is defined as follows. Because of the ellipticity of
is defined as follows. Because of the ellipticity of 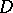 the symbol
the symbol 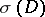 of
of 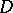 determines an isomorphism of the lifted vector bundles on
determines an isomorphism of the lifted vector bundles on 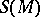 :
:
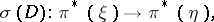 |
where 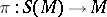 is the bundle of unit spheres of the cotangent bundle
is the bundle of unit spheres of the cotangent bundle 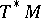 of
of 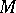 . Let
. Let 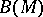 be the bundle of unit balls in
be the bundle of unit balls in 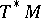 ; this is a
; this is a 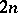 -dimensional manifold with boundary
-dimensional manifold with boundary 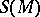 . By glueing the copies
. By glueing the copies 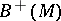 and
and 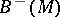 of
of 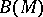 along their common boundary, one obtains a closed
along their common boundary, one obtains a closed 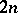 -dimensional manifold
-dimensional manifold  over which the vector bundle
over which the vector bundle
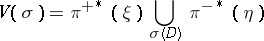 |
is constructed, where 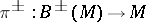 and
and 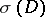 is used to identify
is used to identify 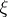 and
and 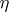 along
along 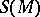 . This vector bundle
. This vector bundle 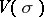 carries all the topological information required for the definition of the topological index. Namely:
carries all the topological information required for the definition of the topological index. Namely:
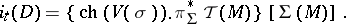 | (2) |
Here 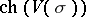 is the cohomological Chern character of the bundle
is the cohomological Chern character of the bundle 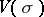 ;
; 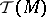 is the cohomological Todd class of the complexified cotangent bundle
is the cohomological Todd class of the complexified cotangent bundle 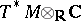 ;
; 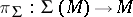 ;
; 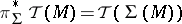 . The right-hand side represents the value of the
. The right-hand side represents the value of the 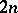 -dimensional component of the element
-dimensional component of the element 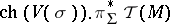 on the fundamental cycle of the manifold
on the fundamental cycle of the manifold 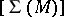 . Thus, the mapping
. Thus, the mapping 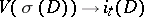 determines a homomorphism
determines a homomorphism 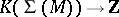 that is trivial on the image of
that is trivial on the image of 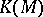 ; here
; here 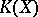 is the Grothendieck group generated by complex vector bundles over
is the Grothendieck group generated by complex vector bundles over 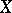 .
.
The Atiyah–Singer index theorem states:
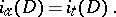 | (3) |
Formula (2) admits a number of modifications. The rational cohomology class 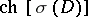 , depending on the symbol
, depending on the symbol 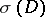 , is introduced as follows. With the triple
, is introduced as follows. With the triple 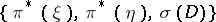 one can associate a difference element (cf. Difference element in
one can associate a difference element (cf. Difference element in 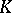 -theory), which can be regarded as the first obstruction to extending the isomorphism
-theory), which can be regarded as the first obstruction to extending the isomorphism 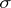 to the whole of
to the whole of 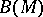 ,
,
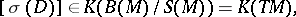 |
where 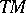 is the tangent bundle, which (by means of the Riemannian metric on
is the tangent bundle, which (by means of the Riemannian metric on 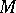 ) can be identified with
) can be identified with 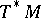 ;
; 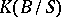 is the relative Grothendieck group of vector bundles over
is the relative Grothendieck group of vector bundles over 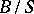 , and hence for the Chern character of
, and hence for the Chern character of 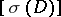 :
: 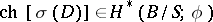 . The formula for the topological index of
. The formula for the topological index of 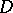 now takes the form:
now takes the form:
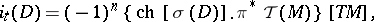 | (4) |
where 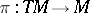 ,
, 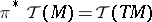 .
.
The Thom isomorphism
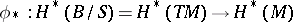 |
then enables one to write (4) in the form
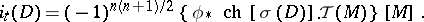 | (5) |
(As before, on the right-hand side of (4) and (5) are the values of the corresponding elements on the fundamental cycles, as in (2).)
The topological index is expressed in terms of 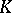 -theory as follows. Let
-theory as follows. Let 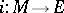 be a differentiable imbedding of
be a differentiable imbedding of 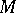 in a Euclidean space,
in a Euclidean space, 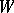 a tubular neighbourhood of
a tubular neighbourhood of 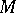 in
in 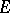 , which can be regarded as a real vector bundle over
, which can be regarded as a real vector bundle over 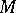 , so that
, so that 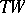 is isomorphic (over
is isomorphic (over 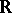 ) to
) to 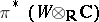 , the complexification of
, the complexification of 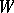 lifted to
lifted to 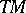 by the projection
by the projection 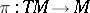 . Composition of the Thom isomorphism
. Composition of the Thom isomorphism 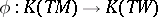 with the natural homomorphism
with the natural homomorphism 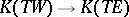 induced by the imbedding
induced by the imbedding 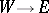 induces a homomorphism
induces a homomorphism 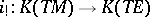 . Let
. Let 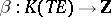 be the Bott periodicity isomorphism. Then the homomorphism
be the Bott periodicity isomorphism. Then the homomorphism 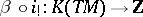 does not depend on the imbedding and
does not depend on the imbedding and
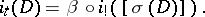 |
Examples.
3) Let  be a closed oriented Riemannian manifold, let
be a closed oriented Riemannian manifold, let 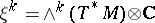 be the bundle of complex exterior
be the bundle of complex exterior 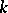 -forms over
-forms over 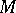 and let
and let
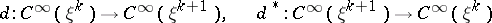 |
be the exterior differentiation operator and its adjoint, respectively. The operator
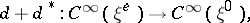 |
where 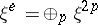 ,
, 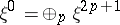 , is elliptic and the index formula (3) holds for it; furthermore the topological index is equal to the Euler characteristic
, is elliptic and the index formula (3) holds for it; furthermore the topological index is equal to the Euler characteristic 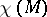 (the Hodge–de Rham theorem). For
(the Hodge–de Rham theorem). For 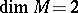 the Gauss–Bonnet theorem follows.
the Gauss–Bonnet theorem follows.
4) Let 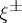 be the eigen
be the eigen 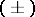 -spaces of the involution
-spaces of the involution 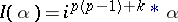 ,
, 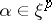 , where
, where  is the duality operator determined by the metric on
is the duality operator determined by the metric on 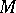 ,
, 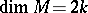 . The restriction of the operator
. The restriction of the operator 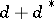 to an operator from
to an operator from 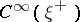 into
into 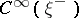 , called the signature operator
, called the signature operator 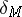 , is an elliptic operator for which the index formula (3) holds; furthermore, the analytic index is equal to the signature of the manifold
, is an elliptic operator for which the index formula (3) holds; furthermore, the analytic index is equal to the signature of the manifold 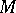 , while the topological index is equal to the
, while the topological index is equal to the 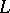 -genus (Hirzebruch's theorem).
-genus (Hirzebruch's theorem).
5) Let 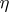 be a holomorphic vector bundle over the complex compact manifold
be a holomorphic vector bundle over the complex compact manifold 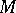 , let
, let 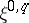 be the bundle of differential forms of type
be the bundle of differential forms of type 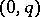 , let
, let 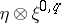 be the bundle of forms of type
be the bundle of forms of type 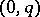 with coefficients in
with coefficients in 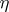 , and let
, and let 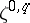 be the
be the 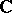 -module of smooth sections of this bundle. Let
-module of smooth sections of this bundle. Let 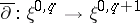 be the Cauchy–Riemann–Dolbeault operator,
be the Cauchy–Riemann–Dolbeault operator, 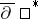 its adjoint, and let
its adjoint, and let 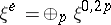 ,
, 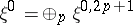 . Then the operator
. Then the operator 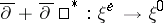 is an elliptic operator for which (3) holds; furthermore, the analytic index is equal to the Euler characteristic of
is an elliptic operator for which (3) holds; furthermore, the analytic index is equal to the Euler characteristic of 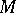 with coefficients in the sheaf of germs of holomorphic sections of
with coefficients in the sheaf of germs of holomorphic sections of 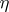 , while the topological index is
, while the topological index is 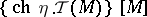 , where
, where 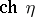 is the Chern character of
is the Chern character of 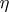 and
and 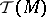 is the Todd class of the tangent bundle to
is the Todd class of the tangent bundle to 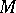 (the Riemann–Roch–Hirzebruch theorem).
(the Riemann–Roch–Hirzebruch theorem).
Elliptic complexes.
In the more general situation which arises naturally, for example, in differential geometry, instead of a single operator 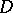 one considers a complex of (pseudo-differential) operators
one considers a complex of (pseudo-differential) operators
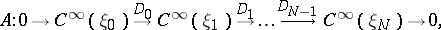 |
where the 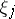 are differentiable vector bundles over the closed manifold
are differentiable vector bundles over the closed manifold 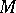 and
and 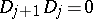 . By the symbol of the complex
. By the symbol of the complex 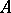 one means the corresponding sequence of principal symbols
one means the corresponding sequence of principal symbols
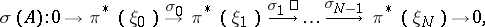 |
where 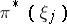 is the lifting of
is the lifting of 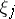 to
to 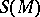 by the projection
by the projection 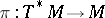 . The complex
. The complex 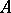 is called elliptic if its symbol is an acyclic complex, that is, if it is exact everywhere outside the zero section. By the analytic index of the complex
is called elliptic if its symbol is an acyclic complex, that is, if it is exact everywhere outside the zero section. By the analytic index of the complex 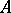 one means its Euler characteristic:
one means its Euler characteristic:
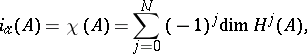 |
where 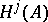 is the
is the 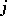 -th cohomology group of
-th cohomology group of 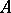 . Two important examples of elliptic complexes are the de Rham complex and its complex analogue, the Dolbeault complex. The problem of computing
. Two important examples of elliptic complexes are the de Rham complex and its complex analogue, the Dolbeault complex. The problem of computing 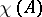 in terms of the class of the complex
in terms of the class of the complex 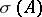 in
in 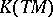 can be reduced to computing the index for a single operator [3].
can be reduced to computing the index for a single operator [3].
If a compact group 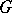 acts on
acts on 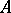 (and commutes with the action of
(and commutes with the action of 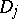 , that is,
, that is, 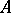 is a
is a 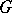 -complex), then
-complex), then 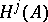 is a
is a 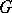 -module, and
-module, and 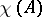 is defined as an element of the ring of characters of the group
is defined as an element of the ring of characters of the group 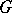 . This is a function in
. This is a function in 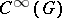 . Here it turns out that the index theorem can be regarded as a generalization of the Lefschetz theorem on fixed points, since the topological index at a point
. Here it turns out that the index theorem can be regarded as a generalization of the Lefschetz theorem on fixed points, since the topological index at a point 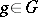 can be expressed in terms of the index of the restriction of the symbol to the subset
can be expressed in terms of the index of the restriction of the symbol to the subset 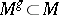 of fixed points of the mapping defined by
of fixed points of the mapping defined by 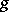 .
.
Let 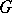 be a topological cyclic group, that is, there exists an element
be a topological cyclic group, that is, there exists an element 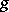 in
in 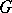 whose powers are dense in
whose powers are dense in 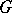 , let
, let 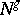 be the normal bundle to
be the normal bundle to 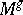 in
in 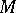 and let
and let 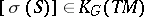 be the class of the symbol of
be the class of the symbol of 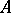 . Let
. Let 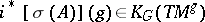 be its restriction and let
be its restriction and let 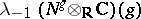 be the class generated by the standard complex of exterior powers of the bundle
be the class generated by the standard complex of exterior powers of the bundle 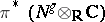 to
to 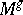 (here
(here 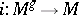 ,
, 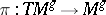 ). Then the Lefschetz number
). Then the Lefschetz number 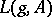 , which is equal to
, which is equal to 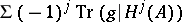 , is given by the formula
, is given by the formula
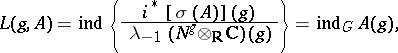 |
where 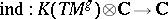 is the natural extension of the topological index
is the natural extension of the topological index 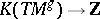 . The cohomological version of this formula is given by:
. The cohomological version of this formula is given by:
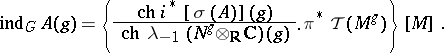 | (6) |
Without the compactness condition on 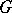 , but under the hypothesis that
, but under the hypothesis that 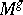 is a zero-dimensional submanifold and that the action of
is a zero-dimensional submanifold and that the action of 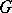 is non-degenerate (that is, the graph of
is non-degenerate (that is, the graph of 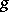 is transversal to the diagonal in
is transversal to the diagonal in 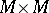 ), there is an analogous formula, which can be expressed as follows. If
), there is an analogous formula, which can be expressed as follows. If 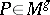 , then
, then 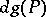 leaves
leaves 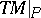 fixed while
fixed while 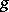 induces a linear mapping
induces a linear mapping 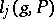 on the fibres
on the fibres 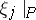 , and
, and
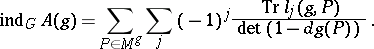 |
Finally, it is possible to weaken the condition of ellipticity of the 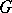 -complex
-complex 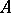 by considering so-called transversally-elliptic complexes; in this case, the index turns out to be a generalized function on the group
by considering so-called transversally-elliptic complexes; in this case, the index turns out to be a generalized function on the group 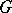 (see [8]). In particular, if
(see [8]). In particular, if 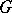 is finite, then transversal ellipticity is to equivalent to ellipticity, so that the previous formulas are applicable. If
is finite, then transversal ellipticity is to equivalent to ellipticity, so that the previous formulas are applicable. If 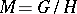 is a homogeneous space, then all the complexes of operators are transversally elliptic and in this case the index formula is in essence the same as the Frobenius reciprocity formula for the induced representations of the group
is a homogeneous space, then all the complexes of operators are transversally elliptic and in this case the index formula is in essence the same as the Frobenius reciprocity formula for the induced representations of the group 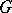 .
.
Non-Fredholm operators.
In this case it is also sometimes possible to give another definition of the analytic index and to obtain corresponding index formulas.
Examples.
6) Let 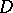 be a uniformly-elliptic operator on
be a uniformly-elliptic operator on 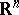 with almost-periodic coefficients. The analytic index
with almost-periodic coefficients. The analytic index 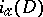 is introduced by means of the relative dimension in the
is introduced by means of the relative dimension in the 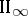 -factor (see von Neumann algebra) and is a real number (see [11]). There is a formula analogous to (1), but instead of the integral over
-factor (see von Neumann algebra) and is a real number (see [11]). There is a formula analogous to (1), but instead of the integral over 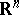 the average value of the almost-periodic function is used.
the average value of the almost-periodic function is used.
7) Suppose that a discrete group 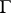 acts freely on a manifold
acts freely on a manifold 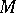 and that the quotient space
and that the quotient space 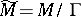 is compact; let
is compact; let 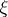 ,
, 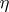 be vector bundles over
be vector bundles over 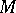 and let
and let 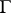 act on them in accordance with its action on
act on them in accordance with its action on 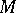 . The analytic index of an elliptic operator
. The analytic index of an elliptic operator 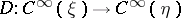 on
on 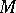 commuting with the action of
commuting with the action of 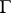 is defined by the formula
is defined by the formula
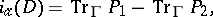 | (7) |
where 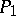 ,
, 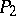 are the orthogonal projections on
are the orthogonal projections on 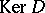 and
and 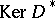 in
in 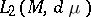 ,
, 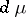 is any
is any 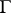 -invariant smooth density on
-invariant smooth density on 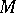 and
and 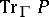 is defined, for any operator
is defined, for any operator 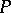 commuting with
commuting with 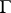 and having smooth kernel
and having smooth kernel 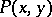 , by the formula
, by the formula
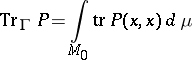 |
(here 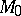 is any fundamental domain of the group
is any fundamental domain of the group 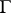 on
on 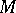 and
and 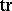 is the trace of the matrix). It turns out that
is the trace of the matrix). It turns out that 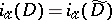 , where
, where 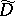 is the operator on
is the operator on 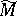 whose symbol
whose symbol 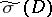 induces
induces 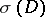 under the lifting to
under the lifting to 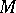 by the canonical projection
by the canonical projection 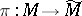 [12]. Thus, the index formula for the operator
[12]. Thus, the index formula for the operator 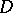 can be obtained from the index formula for the operator
can be obtained from the index formula for the operator 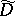 on the compact manifold
on the compact manifold 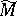 . This result enables one to reveal the non-triviality of spaces in which representations of discrete series are realized [13].
. This result enables one to reveal the non-triviality of spaces in which representations of discrete series are realized [13].
A formula of the same type can be obtained for invariant elliptic operators on homogeneous spaces of Lie groups, even without 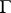 being discrete, with a natural generalization of the analytic index [20].
being discrete, with a natural generalization of the analytic index [20].
Another generalization of this situation can be obtained if one considers invariant operators on a manifold 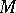 with an action of a locally compact group
with an action of a locally compact group 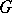 such that
such that 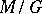 is compact [24].
is compact [24].
8) If the coefficients of a uniformly-elliptic operator 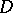 on
on 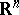 form a homogeneous measurable random field, then it is possible to introduce the analytic index
form a homogeneous measurable random field, then it is possible to introduce the analytic index 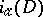 , which is a random variable (in the ergodic case, a real number) defined by formula (7) with
, which is a random variable (in the ergodic case, a real number) defined by formula (7) with 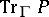 replaced by
replaced by 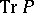 . Here
. Here 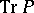 is constructed from the kernel
is constructed from the kernel 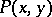 of the operator
of the operator 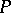 by averaging over
by averaging over  :
: 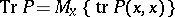 . This example is a generalization of Example 6) and an analogous index formula holds for it .
. This example is a generalization of Example 6) and an analogous index formula holds for it .
9) Let 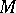 be a compact manifold with a foliation
be a compact manifold with a foliation 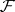 and
and 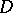 a longitudinal elliptic differential operator on
a longitudinal elliptic differential operator on 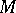 , i.e. a differential operator containing only differentiations along the leaves and elliptic on every leaf. Suppose that there is a transverse measure on
, i.e. a differential operator containing only differentiations along the leaves and elliptic on every leaf. Suppose that there is a transverse measure on 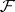 . Then a real-valued analytic index of
. Then a real-valued analytic index of 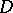 can be defined and a formula of Atiyah–Singer type can be proved. Considering measured foliations, in this context one comes to a formula which generalizes that of Example 8), [18], [19].
can be defined and a formula of Atiyah–Singer type can be proved. Considering measured foliations, in this context one comes to a formula which generalizes that of Example 8), [18], [19].
Index formulas with values in 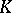 -groups.
-groups.
10) If a family of elliptic operators is given, parametrized by the points 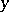 of a compact space
of a compact space 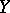 , then its analytic index
, then its analytic index 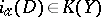 has been defined (see [15]). The topological index
has been defined (see [15]). The topological index 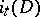 is constructed by analogy with formula (6) (all the constructions are carried out "fibrewise" over
is constructed by analogy with formula (6) (all the constructions are carried out "fibrewise" over 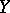 ) and the index theorem holds.
) and the index theorem holds.
11) A more general theorem is obtained if one considers elliptic operators over a compact manifold acting in sections of vector bundles with fibres which are finitely-generated projective modules over a fixed 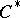 -algebra
-algebra 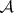 . The analytic index here takes values in the group
. The analytic index here takes values in the group 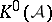 . If one takes
. If one takes 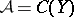 with a compact
with a compact 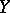 , then one obtains the formula of Example 10). Also the equivalent situation (with a compact Lie group
, then one obtains the formula of Example 10). Also the equivalent situation (with a compact Lie group 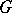 ) can be considered in this context [26], [29].
) can be considered in this context [26], [29].
The case when 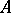 is a
is a 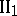 -factor is of particular interest [28], implying the formula of Example 7).
-factor is of particular interest [28], implying the formula of Example 7).
12) There is a number of generalizations of the Atiyah–Singer formulas with the analytic index taking values in homology 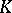 -groups or bivariant Kasparov
-groups or bivariant Kasparov 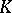 -groups. Taking the Chern character and applying some kind of intersection index usually allows one to pass to the usual number-valued index formulas [23], [25]. Also, the longitudinal index theorem of Example 9) can be generalized in this manner [21].
-groups. Taking the Chern character and applying some kind of intersection index usually allows one to pass to the usual number-valued index formulas [23], [25]. Also, the longitudinal index theorem of Example 9) can be generalized in this manner [21].
13) Consider two generalized Dirac operators 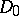 ,
, 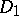 which coincide near infinity (in particular, they are defined on Riemannian manifolds
which coincide near infinity (in particular, they are defined on Riemannian manifolds 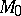 ,
, 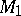 which coincide near infinity, i.e.
which coincide near infinity, i.e. 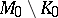 and
and 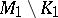 are isometric for some compact subsets
are isometric for some compact subsets 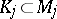 ,
, 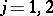 ). Let
). Let 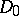 ,
, 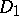 be positive near infinity and let there be the natural splittings
be positive near infinity and let there be the natural splittings
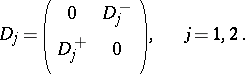 |
Then 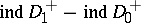 can be expressed by a formula of Atiyah–Singer type having important geometrical applications [22].
can be expressed by a formula of Atiyah–Singer type having important geometrical applications [22].
New analytic tools.
The Atiyah–Bott formula
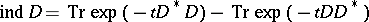 |
provides a local expression of the index if one uses the asymptotic expansion of the traces on the right-hand side as 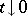 . But this expression contains lower-order terms of the symbol of
. But this expression contains lower-order terms of the symbol of 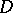 , so it seems difficult to see how the corresponding integrals cancel. It occurred that cancellation is obtained by using some symmetry and supersymmetry arguments. Also a probabilistic approach is effective to work with the traces of heat kernels. Families of elliptic operators can be considered in this way too [30]–[42].
, so it seems difficult to see how the corresponding integrals cancel. It occurred that cancellation is obtained by using some symmetry and supersymmetry arguments. Also a probabilistic approach is effective to work with the traces of heat kernels. Families of elliptic operators can be considered in this way too [30]–[42].
References
| [1] | I.M. Gel'fand, "On elliptic differential equations" Russian Math. Surveys , 15 : 3 (1960) pp. 113–123 Uspekhi Mat. Nauk , 15 : 3 (1960) pp. 121–132 |
| [2] | M.F. Atiyah, I.M. Singer, "The index of elliptic operators on compact manifolds" Bull. Amer. Math. Soc. , 69 (1963) pp. 422–433 |
| [3] | M.F. Atiyah, I.M. Singer, "The index of elliptic operators I" Ann. of Math. , 87 (1968) pp. 484–530 |
| [4] | M.F. Atiyah, G.B. Segal, "The index of elliptic operators II" Ann. of Math. , 87 (1968) pp. 531–545 |
| [5] | M.F. Atiyah, I.M. Singer, "The index of elliptic operators III" Ann. of Math. , 87 (1968) pp. 546–604 |
| [6] | M.F. Atiyah, I.M. Singer, "The index of elliptic operators IV" Ann. of Math. , 93 (1971) pp. 119–138 |
| [7] | B.V. Fedosov, "Analytic formulas for the index of elliptic operators" Trans. Moscow Math. Soc. , 30 (1974) pp. 279–330 Trudy Moskov. Mat. Obshch. , 30 (1974) pp. 159–241 |
| [8] | M.F. Atiyah, "Elliptic operators and compact groups" , Lect. notes in math. , 401 , Springer (1974) |
| [9] | R.S. Palais, "Seminar on the Atiyah–Singer index theorem" , Princeton Univ. Press (1965) |
| [10a] | M.F. Atiyah, R. Bott, V.K. Patodi, "On the heat equation and the index theorem" Invent. Math. , 19 (1973) pp. 279–330 |
| [10b] | M.F. Atiyah, R. Bott, V.K. Patodi, "Errata to "On the heat equation and the index theorem" " Invent. Math. , 28 (1975) pp. 277–280 |
| [11] | L. Coburn, R. Moyer, I.M. Singer, "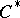 -algebras of almost-periodic pseudo-differential operators" Acta Math. , 130 : 3–4 (1973) pp. 279–307 -algebras of almost-periodic pseudo-differential operators" Acta Math. , 130 : 3–4 (1973) pp. 279–307 |
| [12] | M.F. Atiyah, "Elliptic operators, discrete groups and von Neumann algebras" Astérisque , 32–33 (1976) pp. 43–72 |
| [13] | M.F. Atiyah, W. Schmid, "A geometric construction of the discrete series for semisimple Lie groups" Invent. Math. , 42 (1977) pp. 1–62 |
| [14a] | B.V. Fedosov, M.A. Shubin, "The index of random elliptic operators I" Math. USSR Sb. , 34 (1978) pp. 671–699 Mat. Sb. , 106 : 1 pp. 108–140 |
| [14b] | B.V. Fedosov, M.A. Shubin, "The index of random elliptic operators II" Math. USSR Sb. , 35 (1979) pp. 131–156 Mat. Sb. , 106 : 3 pp. 455–483 |
| [15] | M.F. Atiyah, "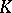 -theory: lectures" , Benjamin (1967) -theory: lectures" , Benjamin (1967) |
| [16] | L. Boutet de Monvel, "Boundary problems for pseudodifferential operators" Acta Math. , 126 : 1–2 (1971) pp. 11–51 |
| [17a] | B.V. Fedosov, "The analytic formula for the index of an elliptic boundary value problem" Mat. USSR Sb. , 22 (1974) pp. 61–90 Mat. Sb. , 93 : 1 (1974) pp. 62–89 |
| [17b] | B.V. Fedosov, "An analytic formula for the index of an elliptic boundary value problem II" Mat. USSR Sb. , 24 (1974) pp. 511–535 Mat. Sb. , 95 : 4 (1974) pp. 525–550 |
| [17c] | B.V. Fedosov, "An analytic formula for the index of an elliptic boundary value problem III" Mat. USSR Sb. , 30 (1976) pp. 341–359 Mat. Sb. , 101 : 3 (1976) pp. 380–401 |
| [18] | A. Connes, "Sur la théorie non commutative de l'intégration" , Algèbres d'opérateurs , Lect. notes in math. , 725 , Springer (1979) pp. 19–143 |
| [19] | A. Connes, "A survey of foliations and operator algebras" , Operator algebras and applications , Proc. Symp. Pure Math. , 38 : 1 , Amer. Math. Soc. (1982) pp. 521–628 |
| [20] | A. Connes, H. Moscovici, "The 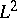 -index theorem for homogeneous spaces of Lie groups" Ann. of Math. , 115 (1982) pp. 291–330 -index theorem for homogeneous spaces of Lie groups" Ann. of Math. , 115 (1982) pp. 291–330 |
| [21] | A. Connes, G. Skandalis, "The longitudinal index theorem for foliations" Publ. Res. Inst. Math. Sci. Kyoto Univ. , 20 (1984) pp. 1139–1183 |
| [22] | M. Gromov, H.B. Lawson, "Positive scalar curvature and the Dirac operator on complete Riemannian manifolds" Publ. Math. IHES , 58 (1983) pp. 83–196 |
| [23] | G.G. Kasparov, "Topological invariants of elliptic operators I. 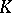 -homology" Math. USSR Izv. , 9 (1975) pp. 751–792 Izv. Akad. Nauk SSSR, Ser. Mat. , 39 (1975) pp. 796–838 -homology" Math. USSR Izv. , 9 (1975) pp. 751–792 Izv. Akad. Nauk SSSR, Ser. Mat. , 39 (1975) pp. 796–838 |
| [24] | G.G. Kasparov, "An index of invariant elliptic operators, 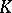 -theory, and representations of Lie groups" Soviet Math. Dokl. , 27 (1983) pp. 105–109 Dokl. Akad. Nauk SSSR , 268 (1983) pp. 533–537 -theory, and representations of Lie groups" Soviet Math. Dokl. , 27 (1983) pp. 105–109 Dokl. Akad. Nauk SSSR , 268 (1983) pp. 533–537 |
| [25] | G.G. Kasparov, "Operator 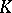 -theory and its applications: elliptic operators, group representation, higher signatures, -theory and its applications: elliptic operators, group representation, higher signatures, 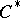 -extensions" , Proc. Internat. Congress Mathematicians (Warszawa, 1983) , PWN & Elsevier (1984) pp. 987–1000 -extensions" , Proc. Internat. Congress Mathematicians (Warszawa, 1983) , PWN & Elsevier (1984) pp. 987–1000 |
| [26] | A.S. [A.S. Mishchenko] Miščenko, A.T. Fomenko, "The index of elliptic operators over 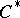 -algebras" Math. USSR Izv. , 15 (1980) pp. 87–112 Izv. Akad. Nauk SSSR, Ser. Mat. , 43 (1979) pp. 831–851 -algebras" Math. USSR Izv. , 15 (1980) pp. 87–112 Izv. Akad. Nauk SSSR, Ser. Mat. , 43 (1979) pp. 831–851 |
| [27] | S. Rempel, B.-W. Schulze, "Index theory of elliptic boundary problems" , Akademie Verlag (1982) |
| [28] | I.M. Singer, "Some remarks on operator theory and index theory" , 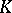 -theory and operator algebras , Lect. notes in math. , 757 , Springer (1977) pp. 128–138 -theory and operator algebras , Lect. notes in math. , 757 , Springer (1977) pp. 128–138 |
| [29] | E.V. Troitskii, "The equivariant index of 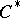 -elliptic operators" Math. USSR Izv. , 29 (1987) pp. 207–224 Izv. Akad. Nauk SSSR, Ser. Mat. , 50 (1986) pp. 849–965 -elliptic operators" Math. USSR Izv. , 29 (1987) pp. 207–224 Izv. Akad. Nauk SSSR, Ser. Mat. , 50 (1986) pp. 849–965 |
| [30] | L. Alvarez-Gaumé, "Supersymmetry and the Atiyah–Singer index theorem" Commun. Math. Phys. , 90 (1983) pp. 161–173 |
| [31] | D. Quillen, "Superconnections and the Chern character" Topology , 24 (1985) pp. 89–95 |
| [32] | N. Berline, M. Vergne, "A computation of the equivariant index of the Dirac operator" Bull. Soc. Math. France , 113 (1985) pp. 305–345 |
| [33] | N. Berline, M. Vergne, "A proof of Bismut local index theorem for a family of Dirac operators" Topology , 26 (1987) pp. 435–464 |
| [34] | J.-M. Bismut, "The Atiyah–Singer theorem: A probabilistic approach I. The index theorem" J. Funct. Anal. , 57 (1984) pp. 56–98 |
| [35] | J.-M. Bismut, "Localization formulas, superconnections, and the index theorem for families" Commun. Math. Phys. , 103 (1986) pp. 127–166 |
| [36] | J.-M. Bismut, "The Atiyah–Singer index theorem for families of Dirac operators: two heat equation proofs" Invent. Math. , 83 (1986) pp. 91–151 |
| [37] | H. Donnelly, "Local index theorem for families" Michigan Math. J. , 35 (1988) pp. 11–20 |
| [38] | E. Getzler, "Pseudodifferential operators on supermanifolds and the Atiyah–Singer index theorem" Commun. Math. Phys. , 92 (1983) pp. 163–178 |
| [39] | E. Getzler, "A short proof of the local Atiyah–Singer index theorem" Topology , 25 (1988) pp. 111–117 |
| [40] | P. Gilkey, "Invariance theory, the heat equation and the Atiyah–Singer theorem" , Publish or Perish (1984) |
| [41] | R. Léandre, "Sur le théorème d'Atiyah–Singer" Probab. Theory Related Fields , 80 (1988) pp. 119–137 |
| [42] | R. Léandre, "Sur le théorème de l'indice des familles" , Sem. Probab. Strasbourg XII , Lect. notes in math. , 1321 , Springer (1988) pp. 348–413 |
Comments
Several new proofs of the Atiyah–Singer index theorem have been given in recent years.
In his paper [a5], E. Witten suggested that supersymmetric quantum theory might provide the framework for a simple proof of the index theorem. Such a proof was realized by L. Alvarez-Gaumé [30] and subsequently by Friedan and Windey [a4]. These theoretical physicists relied on formal manipulations inside path integrals (including fermionic path integrals). So their proofs were certainly not rigorous. E. Getzler [38] found a rigorous version of their arguments which relied on pseudo-differential operator theory and the theory of supermanifolds. More recently, Getzler [39] found a proof whose geometric and algebraic parts are elementary and transparent. Independent of this work J.-M. Bismut [34] found a related proof using probabilistic methods.
For further material cf. also [a2], Chapt. XIX, [a1], Chapt. 12 and [a3], Chapt. 9.
References
| [a1] | H.L. Cycon, R.G. Froese, W. Kirsch, B. Simon, "Schrödinger operators" , Springer (1987) |
| [a2] | L.V. Hörmander, "The analysis of linear partial differential operators" , III. Pseudo-differential operators , Springer (1985) |
| [a3] | M. Kaku, "Introduction to superstrings" , Springer (1988) |
| [a4] | D. Friedan, P. Windey, "Supersymmetric derivation of the Atiyah–Singer index theorem and the chiral anomaly" Nucl. Phys. , B253 (1984) pp. 395–416 |
| [a5] | E. Witten, "Supersymmetry and Morse theory" J. Diff. Geom. , 17 (1982) pp. 661–692 |
Index formulas. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Index_formulas&oldid=18079