of a number  modulo
modulo 
The exponent  in the congruence
in the congruence  , where
, where  and
and  are relatively prime integers and
are relatively prime integers and  is a fixed primitive root modulo
is a fixed primitive root modulo  . The index of
. The index of  modulo
modulo  is denoted by
is denoted by 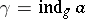 , or
, or 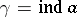 for short. Primitive roots exist only for moduli of the form
for short. Primitive roots exist only for moduli of the form 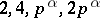 , where
, where 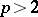 is a prime number; consequently, the notion of an index is only defined for these moduli.
is a prime number; consequently, the notion of an index is only defined for these moduli.
If 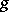 is a primitive root modulo
is a primitive root modulo 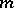 and
and 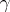 runs through the values
runs through the values 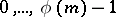 , where
, where 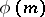 is the Euler function, then
is the Euler function, then  runs through a reduced system of residues modulo
runs through a reduced system of residues modulo  . Consequently, for each number relatively prime with
. Consequently, for each number relatively prime with 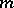 there exist a unique index
there exist a unique index 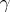 for which
for which  . Any other index
. Any other index 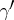 of
of  satisfies the congruence
satisfies the congruence 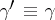
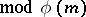 . Therefore, the indices of
. Therefore, the indices of  form a residue class modulo
form a residue class modulo  .
.
The notion of an index is analogous to that of a logarithm of a number, and the index satisfies a number of properties of the logarithm, namely:
where  denotes the root of the equation
denotes the root of the equation
If  is the canonical factorization of an arbitrary natural number
is the canonical factorization of an arbitrary natural number  and
and  are primitive roots modulo
are primitive roots modulo  , respectively, then for each
, respectively, then for each  relatively primitive with
relatively primitive with  there exist integers
there exist integers  for which
for which
The above system 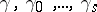 is called a system of indices of
is called a system of indices of  modulo
modulo 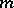 . To each number
. To each number  relatively prime with
relatively prime with 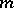 corresponds a unique system of indices
corresponds a unique system of indices  for which
for which
where  ,
,  , and
, and  and
and  and defined as follows:
and defined as follows:
Every other system 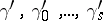 of indices of
of indices of  satisfies the congruences
satisfies the congruences
The notion of a system of indices of  modulo
modulo  is convenient for the explicit construction of characters of the multiplicative group of reduced residue classes modulo
is convenient for the explicit construction of characters of the multiplicative group of reduced residue classes modulo  .
.
References
| [1] | I.M. Vinogradov, "Elements of number theory" , Dover, reprint (1954) (Translated from Russian) |
References
| [a1] | H. Davenport, "Multiplicative number theory" , Springer (1980) |
How to Cite This Entry:
Index. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Index&oldid=17202
This article was adapted from an original article by S.A. Stepanov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098.
See original article modulo
modulo 
 in the congruence
in the congruence  , where
, where  and
and  are relatively prime integers and
are relatively prime integers and  is a fixed primitive root modulo
is a fixed primitive root modulo  . The index of
. The index of  modulo
modulo  is denoted by
is denoted by 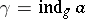 , or
, or 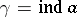 for short. Primitive roots exist only for moduli of the form
for short. Primitive roots exist only for moduli of the form 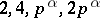 , where
, where 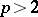 is a prime number; consequently, the notion of an index is only defined for these moduli.
is a prime number; consequently, the notion of an index is only defined for these moduli.
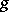 is a primitive root modulo
is a primitive root modulo 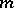 and
and 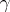 runs through the values
runs through the values 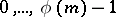 , where
, where 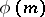 is the Euler function, then
is the Euler function, then  runs through a reduced system of residues modulo
runs through a reduced system of residues modulo  . Consequently, for each number relatively prime with
. Consequently, for each number relatively prime with 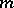 there exist a unique index
there exist a unique index 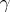 for which
for which  . Any other index
. Any other index 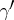 of
of  satisfies the congruence
satisfies the congruence 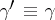
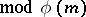 . Therefore, the indices of
. Therefore, the indices of  form a residue class modulo
form a residue class modulo  .
.
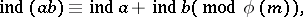

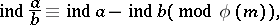
 denotes the root of the equation
denotes the root of the equation

 is the canonical factorization of an arbitrary natural number
is the canonical factorization of an arbitrary natural number 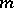 and
and  are primitive roots modulo
are primitive roots modulo  , respectively, then for each
, respectively, then for each  relatively primitive with
relatively primitive with  there exist integers
there exist integers 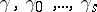 for which
for which
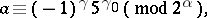
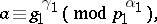

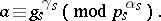
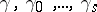 is called a system of indices of
is called a system of indices of  modulo
modulo 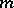 . To each number
. To each number  relatively prime with
relatively prime with 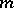 corresponds a unique system of indices
corresponds a unique system of indices  for which
for which
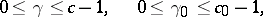
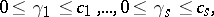
 ,
,  , and
, and  and
and  and defined as follows:
and defined as follows:

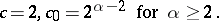
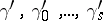 of indices of
of indices of  satisfies the congruences
satisfies the congruences

 modulo
modulo  is convenient for the explicit construction of characters of the multiplicative group of reduced residue classes modulo
is convenient for the explicit construction of characters of the multiplicative group of reduced residue classes modulo  .
.