Indefinite integral
An integral
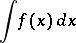 | (*) |
of a given function of a single variable defined on some interval. It is the collection of all primitives of the given function on this interval. If 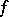 is defined on an interval
is defined on an interval  of the real axis and
of the real axis and 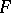 is any primitive of it on
is any primitive of it on 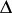 , that is,
, that is, 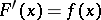 for all
for all 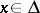 , then any other primitive of
, then any other primitive of 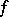 on
on 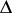 is of the form
is of the form 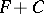 , where
, where 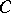 is a constant. Consequently, the indefinite integral (*) consists of all functions of the form
is a constant. Consequently, the indefinite integral (*) consists of all functions of the form 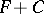 .
.
The indefinite Lebesgue integral of a summable function on 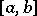 is the collection of all functions of the form
is the collection of all functions of the form
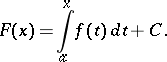 |
In this case the equality 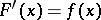 holds, generally speaking, only almost-everywhere on
holds, generally speaking, only almost-everywhere on 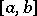 .
.
An indefinite Lebesgue integral (in the wide sense) of a summable function 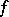 defined on a measure space
defined on a measure space 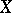 with measure
with measure 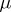 is the name for the set function
is the name for the set function
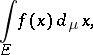 |
defined on the collection of all measurable sets 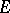 in
in 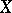 .
.
References
| [1] | A.N. Kolmogorov, S.V. Fomin, "Elements of the theory of functions and functional analysis" , 1–2 , Graylock (1957–1961) (Translated from Russian) |
| [2] | S.M. Nikol'skii, "A course of mathematical analysis" , 1–2 , MIR (1977) (Translated from Russian) |
| [3] | V.A. Il'in, E.G. Poznyak, "Fundamentals of mathematical analysis" , 1–2 , MIR (1982) (Translated from Russian) |
Comments
For additional references see Improper integral; Integral.
Indefinite integral. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Indefinite_integral&oldid=11527