Imbedding of semi-groups
into groups
A monomorphism of a semi-group into a group. A semi-group 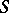 is imbeddable in a group
is imbeddable in a group 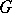 if
if 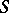 is isomorphic to a sub-semi-group of
is isomorphic to a sub-semi-group of 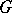 . Necessary and sufficient conditions for imbeddability of a semi-group into a group were found by A.I. Mal'tsev [1] (see also [3]). These conditions form an infinite system of conditional identities (or quasi-identities, cf. Quasi-identity), in particular, the following ones:
. Necessary and sufficient conditions for imbeddability of a semi-group into a group were found by A.I. Mal'tsev [1] (see also [3]). These conditions form an infinite system of conditional identities (or quasi-identities, cf. Quasi-identity), in particular, the following ones:
 |
(cancellation laws);
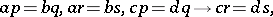 |
where  are elements of the semi-group. The class of semi-groups imbeddable in groups cannot be characterized by a finite system of conditional identities [2]. A number of sufficient conditions for imbeddability of a semi-group into a group are known. The most important ones are the following. If
are elements of the semi-group. The class of semi-groups imbeddable in groups cannot be characterized by a finite system of conditional identities [2]. A number of sufficient conditions for imbeddability of a semi-group into a group are known. The most important ones are the following. If 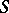 is a semi-group with cancellation and if for any elements
is a semi-group with cancellation and if for any elements  of
of 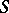 there exist elements
there exist elements 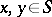 such that
such that 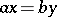 (Ore's condition), then
(Ore's condition), then 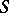 is imbeddable in a group. If
is imbeddable in a group. If 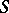 is a semi-group with cancellation in which it always follows from the equality
is a semi-group with cancellation in which it always follows from the equality 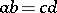 that either
that either 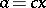 or
or 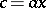 for some element
for some element 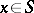 , then
, then 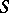 is imbeddable in a group [4]. Sufficient conditions for imbeddability, formulated in the language of graph theory (cf., for example, [5]), are known.
is imbeddable in a group [4]. Sufficient conditions for imbeddability, formulated in the language of graph theory (cf., for example, [5]), are known.
References
| [1] | A.I. Mal'tsev, "On inclusion of associative systems in a group" Mat. Sb. , 6 (48) : 2 (1939) pp. 331–336 (In Russian) (German abstract) |
| [2] | A.I. Mal'tsev, "On inclusion of associative systems in a group II" Mat. Sb. , 8 (50) : 2 (1940) pp. 251–264 (In Russian) |
| [3] | P.M. Cohn, "Universal algebra" , Reidel (1981) |
| [4] | R. Doss, "Sur l'immersion d'une semi-groupe dans une groupe" Bull. Sci. Math. (2) , 72 (1948) pp. 139–150 |
| [5] | S.I. [S.I. Adyan] Adjan, "Defining relations and algorithmic problems for groups and semigroups" Proc. Steklov Inst. Math. , 85 (1967) Trudy Mat. Inst. Steklov. , 85 (1966) |
Comments
Instead of imbedding the word embedding is also used.
References
| [a1] | A.H. Clifford, G.B. Preston, "Algebraic theory of semi-groups" , 1–2 , Amer. Math. Soc. (1961–1967) |
Imbedding of semi-groups. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Imbedding_of_semi-groups&oldid=14833