Hyperbolic trigonometry
From Encyclopedia of Mathematics
The trigonometry on the Lobachevskii plane (cf. Lobachevskii geometry). Let  ,
,  , be the lengths of the sides of a triangle on the Lobachevskii plane, and let
, be the lengths of the sides of a triangle on the Lobachevskii plane, and let  be the angles of this triangle. The following relationship (the cosine theorem), which relates
be the angles of this triangle. The following relationship (the cosine theorem), which relates  with
with  , is valid:
, is valid:
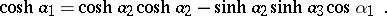 |
All the remaining relations of hyperbolic trigonometry follow from this one, such as the so-called sine theorem:
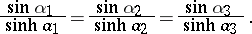 |
Comments
References
| [a1] | H.S.M. Coxeter, "Non-Euclidean geometry" , Univ. Toronto Press (1965) pp. 224–240 |
| [a2] | H.S.M. Coxeter, "Angles and arcs in the hyperbolic plane" Math. Chronicle (New Zealand) , 9 (1980) pp. 17–33 |
How to Cite This Entry:
Hyperbolic trigonometry. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hyperbolic_trigonometry&oldid=19080
Hyperbolic trigonometry. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hyperbolic_trigonometry&oldid=19080
This article was adapted from an original article by A.B. Ivanov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article