Hyperbolic metric
hyperbolic measure
A metric in a domain of the complex plane with at least three boundary points that is invariant under automorphisms of this domain.
The hyperbolic metric in the disc 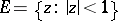 is defined by the line element
is defined by the line element
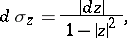 |
where 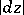 is the line element of Euclidean length. The introduction of the hyperbolic metric in
is the line element of Euclidean length. The introduction of the hyperbolic metric in 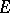 leads to a model of Lobachevskii geometry. In this model the role of straight lines is played by Euclidean circles orthogonal to
leads to a model of Lobachevskii geometry. In this model the role of straight lines is played by Euclidean circles orthogonal to  and lying in
and lying in 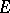 ; the circle
; the circle  plays the role of the improper point. Fractional-linear transformations of
plays the role of the improper point. Fractional-linear transformations of 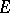 onto itself serve as the motions in it. The hyperbolic length of a curve
onto itself serve as the motions in it. The hyperbolic length of a curve 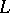 lying inside
lying inside 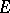 is defined by the formula
is defined by the formula
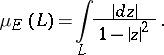 |
The hyperbolic distance between two points 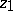 and
and 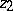 of
of 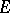 is
is
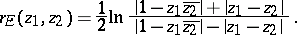 |
The set of points of 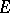 whose hyperbolic distance from
whose hyperbolic distance from 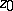 ,
, 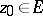 , does not exceed a given number
, does not exceed a given number 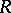 ,
, 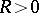 , i.e. the hyperbolic disc in
, i.e. the hyperbolic disc in 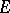 with hyperbolic centre at
with hyperbolic centre at 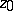 and hyperbolic radius
and hyperbolic radius 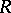 , is a Euclidean disc with centre other than
, is a Euclidean disc with centre other than 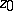 if
if 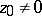 .
.
The hyperbolic area of a domain 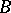 lying in
lying in 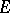 is defined by the formula
is defined by the formula
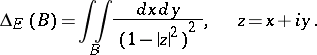 |
The quantities 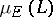 ,
, 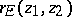 and
and 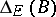 are invariant with respect to fractional-linear transformations of
are invariant with respect to fractional-linear transformations of 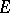 onto itself.
onto itself.
The hyperbolic metric in any domain 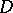 of the
of the  -plane with at least three boundary points is defined as the pre-image of the hyperbolic metric in
-plane with at least three boundary points is defined as the pre-image of the hyperbolic metric in 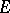 under the conformal mapping
under the conformal mapping 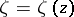 of
of 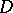 onto
onto  ; its line element is defined by the formula
; its line element is defined by the formula
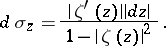 |
A domain with at most two boundary points can no longer be conformally mapped onto a disc. The quantity
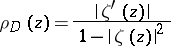 |
is called the density of the hyperbolic metric of 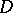 . The hyperbolic metric of a domain
. The hyperbolic metric of a domain 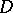 does not depend on the selection of the mapping function or of its branch, and is completely determined by
does not depend on the selection of the mapping function or of its branch, and is completely determined by 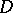 . The hyperbolic length of a curve
. The hyperbolic length of a curve  located in
located in  is found by the formula
is found by the formula
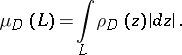 |
The hyperbolic distance between two points 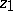 and
and 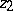 in a domain
in a domain 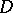 is
is
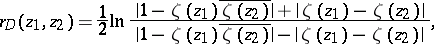 |
where 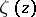 is any function conformally mapping
is any function conformally mapping 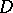 onto
onto 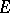 . A hyperbolic circle in
. A hyperbolic circle in 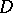 is, as in the case of the disc
is, as in the case of the disc 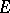 , a set of points in
, a set of points in 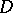 whose hyperbolic distance from a given point of
whose hyperbolic distance from a given point of 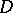 (the hyperbolic centre) does not exceed a given positive number (the hyperbolic radius). If the domain
(the hyperbolic centre) does not exceed a given positive number (the hyperbolic radius). If the domain 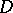 is multiply connected, a hyperbolic circle in
is multiply connected, a hyperbolic circle in 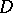 is usually a multiply-connected domain. The hyperbolic area of a domain
is usually a multiply-connected domain. The hyperbolic area of a domain 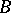 lying in
lying in 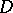 is found by the formula
is found by the formula
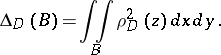 |
The quantities 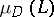 ,
, 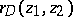 and
and  are invariant under conformal mappings of
are invariant under conformal mappings of 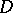 (one of the main properties of the hyperbolic metric in
(one of the main properties of the hyperbolic metric in 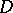 ).
).
References
| [1] | G.M. Goluzin, "Geometric theory of functions of a complex variable" , Transl. Math. Monogr. , 26 , Amer. Math. Soc. (1969) (Translated from Russian) |
| [2] | S. Stoilov, "The theory of functions of a complex variable" , 1–2 , Moscow (1962) (In Russian; translated from Rumanian) |
Comments
Generalizations to higher-dimensional domains (mainly strongly pseudo-convex domains) are, e.g., the Carathéodory metric, the Kobayashi metric and the Bergman metric (for the latter see Bergman kernel function).
Let 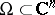 be a domain,
be a domain, 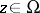 and
and 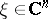 . Denote by
. Denote by  the set of holomorphic mappings
the set of holomorphic mappings 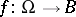 ,
,  the unit ball in
the unit ball in 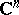 . Then the (infinitesimal version of the) Carathéodory metric is
. Then the (infinitesimal version of the) Carathéodory metric is
 |
and the (infinitesimal version of the) Kobayashi distance is
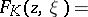 |
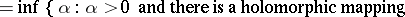 |
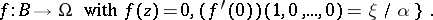 |
Instead of 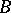 sometimes other domains (e.g. the unit polydisc) are taken. (See [a2], [a3].)
sometimes other domains (e.g. the unit polydisc) are taken. (See [a2], [a3].)
One correspondingly defines for these metrics distance and area.
References
| [a1] | L.V. Ahlfors, "Conformal invariants. Topics in geometric function theory" , McGraw-Hill (1973) |
| [a2] | S. Lang, "Introduction to complex hyperbolic spaces" , Springer (1987) |
| [a3] | S.G. Krantz, "Function theory of several complex variables" , Wiley (1982) |
Hyperbolic metric. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hyperbolic_metric&oldid=17817