Hopf invariant
An invariant of a homotopy class of mappings of topological spaces. It was first defined by H. Hopf ([1], [2]) for mappings of spheres 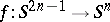 .
.
Let  be a continuous mapping. By transition, if necessary, to a homotopic mapping, one may assume that this mapping is simplicial with respect to certain triangulations of the spheres
be a continuous mapping. By transition, if necessary, to a homotopic mapping, one may assume that this mapping is simplicial with respect to certain triangulations of the spheres 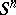 and
and 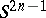 . Then the Hopf invariant is defined as the linking coefficient of the
. Then the Hopf invariant is defined as the linking coefficient of the 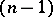 -dimensional disjoint submanifolds
-dimensional disjoint submanifolds 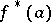 and
and 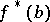 in
in 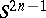 for any distinct
for any distinct 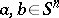 .
.
The mapping 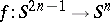 determines an element
determines an element  , and the image of the element
, and the image of the element 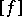 under the homomorphism
under the homomorphism
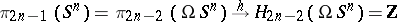 |
coincides with the Hopf invariant 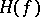 (here
(here 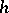 is the Hurewicz homomorphism) [3].
is the Hurewicz homomorphism) [3].
Suppose now that 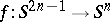 is a mapping of class
is a mapping of class 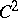 and that a form
and that a form 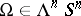 is a generator of the integral cohomology group
is a generator of the integral cohomology group 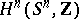 . For such a form one may take, for example,
. For such a form one may take, for example, 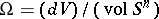 , where
, where 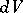 is the volume element on
is the volume element on 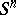 in some metric (for example, in the metric given by the imbedding
in some metric (for example, in the metric given by the imbedding  ), and
), and 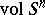 is the volume of the sphere
is the volume of the sphere  . Then the form
. Then the form 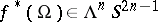 is closed and it is exact because the group
is closed and it is exact because the group  is trivial. Thus,
is trivial. Thus, 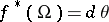 for some form
for some form 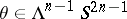 . A formula for the computation of the Hopf invariant is (see [4]):
. A formula for the computation of the Hopf invariant is (see [4]):
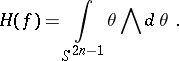 |
The definition of the Hopf invariant can be generalized (see [5], [6]) to the case of mappings 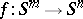 for
for 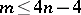 . In this case there is a decomposition
. In this case there is a decomposition
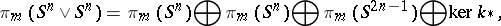 | (*) |
where
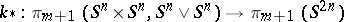 |
is the homomorphism induced by the projection 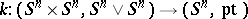 . Let
. Let 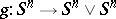 be the mapping given by contracting the equator of the sphere
be the mapping given by contracting the equator of the sphere 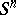 to a point. Then the Hopf invariant is defined as the homomorphism
to a point. Then the Hopf invariant is defined as the homomorphism
 |
under which 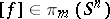 is transformed to the projection of the element
is transformed to the projection of the element 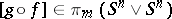 onto the direct summand
onto the direct summand 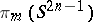 in the decomposition (*). Since
in the decomposition (*). Since 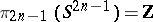 , for
, for  one obtains the usual Hopf invariant. The generalized Hopf invariant is defined as the composite
one obtains the usual Hopf invariant. The generalized Hopf invariant is defined as the composite 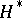 of the homomorphisms
of the homomorphisms
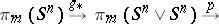 |
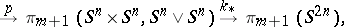 |
where 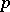 is the projection of the group
is the projection of the group 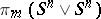 onto the direct summand
onto the direct summand 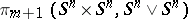 , and the homomorphisms
, and the homomorphisms 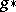 and
and 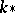 are described above. For
are described above. For 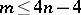 the Hopf–Whitehead invariant
the Hopf–Whitehead invariant 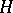 and the Hopf–Hilton invariant
and the Hopf–Hilton invariant 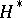 are connected by the relation
are connected by the relation 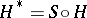 , where
, where 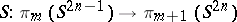 is the suspension homomorphism (see [6]).
is the suspension homomorphism (see [6]).
Let 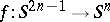 be a mapping and let
be a mapping and let 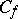 be its cylinder (cf. Mapping cylinder). Then the cohomology space
be its cylinder (cf. Mapping cylinder). Then the cohomology space 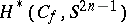 has as homogeneous
has as homogeneous 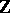 -basis a pair
-basis a pair 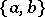 with
with  and
and 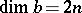 . Here the relation
. Here the relation 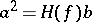 holds (see [7]). If
holds (see [7]). If  is odd, then
is odd, then 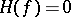 (because multiplication in cohomology is skew-commutative).
(because multiplication in cohomology is skew-commutative).
There is (see [8]) a generalization of the Hopf–Steenrod invariant in terms of a generalized cohomology theory (cf. Generalized cohomology theories). Let 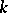 be the semi-exact homotopy functor in the sense of Dold (see [9]), given on the category of finite CW-complexes and taking values in a certain Abelian category
be the semi-exact homotopy functor in the sense of Dold (see [9]), given on the category of finite CW-complexes and taking values in a certain Abelian category 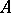 . Then the mapping of complexes
. Then the mapping of complexes 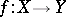 determines an element
determines an element  , where
, where 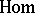 is the set of morphisms in
is the set of morphisms in 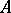 . The Hopf–Adams invariant
. The Hopf–Adams invariant 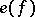 is defined when
is defined when 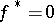 and
and 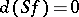 , where
, where 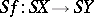 is the corresponding suspension mapping. In this case the sequence of cofibrations
is the corresponding suspension mapping. In this case the sequence of cofibrations
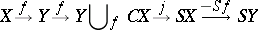 |
corresponds to an exact sequence in 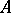 :
:
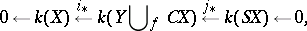 |
which determines the Hopf–Adams–Steenrod invariant 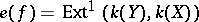 .
.
In the case of the functor  taking values in the category of modules over the Steenrod algebra modulo 2, one obtains the Hopf–Steenrod invariant
taking values in the category of modules over the Steenrod algebra modulo 2, one obtains the Hopf–Steenrod invariant 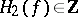 of a mapping
of a mapping 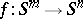 for
for 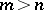 (see [7]). The cohomology space
(see [7]). The cohomology space 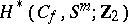 has as
has as 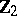 -basis a pair
-basis a pair 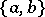 with
with 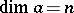 and
and 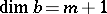 , and then
, and then
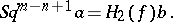 |
The Hopf invariant 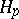 modulo
modulo 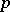 (where
(where 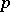 is a prime number) is defined as the composite of the mappings
is a prime number) is defined as the composite of the mappings
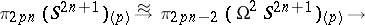 |
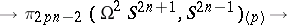 |
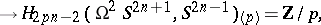 |
where 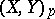 is the localization by
is the localization by 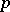 of the pair of spaces (see [10]). Let
of the pair of spaces (see [10]). Let
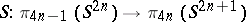 |
be the suspension homomorphism. Then 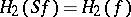 (see [10]). The Hopf invariant
(see [10]). The Hopf invariant 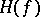 can also be defined in terms of the Stiefel numbers (cf. Stiefel number) (see [11]): If
can also be defined in terms of the Stiefel numbers (cf. Stiefel number) (see [11]): If 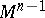 is a closed equipped manifold and if
is a closed equipped manifold and if 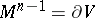 , then the characteristic Stiefel–Whitney number
, then the characteristic Stiefel–Whitney number 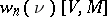 of the normal bundle
of the normal bundle  is the same as the Hopf invariant
is the same as the Hopf invariant 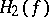 of the mapping
of the mapping 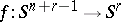 that is a representative of the class of equipped cobordisms of
that is a representative of the class of equipped cobordisms of 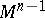 .
.
The Adams–Novikov spectral sequence makes it possible to construct higher Hopf invariants. Namely, one defines inductively the invariants 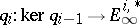 and
and 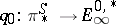 (see [12]). From the form of the differentials of this spectral sequence it follows that
(see [12]). From the form of the differentials of this spectral sequence it follows that
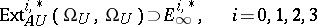 |
(where 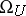 is the ring of complex point cobordisms); therefore, for
is the ring of complex point cobordisms); therefore, for 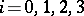 , the invariants
, the invariants 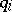 lie in
lie in 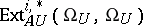 and are called the Hopf–Novikov invariants. For
and are called the Hopf–Novikov invariants. For  one obtains the Adams invariant.
one obtains the Adams invariant.
The values that a Hopf invariant can take are not arbitrary. For example, for a mapping  the Hopf invariant is always 0. The Hopf invariant modulo
the Hopf invariant is always 0. The Hopf invariant modulo 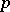 ,
,  , is trivial, except when
, is trivial, except when 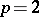 ,
,  and
and 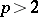 ,
, 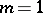 . On the other hand, for any even number
. On the other hand, for any even number  there exists a mapping
there exists a mapping 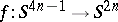 with Hopf invariant
with Hopf invariant  (
( is arbitrary). For
is arbitrary). For 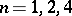 there exists mappings
there exists mappings 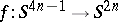 with Hopf invariant 1.
with Hopf invariant 1.
References
| [1] | H. Hopf, "Ueber die Abbildungen der dreidimensionalen Sphäre auf die Kügelfläche" Math. Ann. , 104 (1931) pp. 639–665 |
| [2] | H. Hopf, "Ueber die Abbildungen von Sphären niedriger Dimension" Fund. Math. , 25 (1935) pp. 427–440 |
| [3] | J.-.P. Serre, "Groupes d'homotopie et classes de groupes abéliens" Ann. of Math. , 58 : 2 (1953) pp. 258–294 |
| [4] | J.H.C. Whitehead, "An expression of the Hopf invariant as an integral" Proc. Nat. Acad. Sci. USA , 33 (1937) pp. 117–123 |
| [5] | J.H.C. Whitehead, "A generation of the Hopf invariant" Ann. of Math. (2) , 51 (1950) pp. 192–237 |
| [6] | P. Hilton, "Suspension theorem and generalized Hopf invariant" Proc. London. Math. Soc. (3) , 1 : 3 (1951) pp. 462–493 |
| [7] | N. Steenrod, "Cohomologies invariants of mappings" Ann. of Math. (2) , 50 (1949) pp. 954–988 |
| [8] | J. Adams, "On the groups 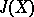 " Topology , 5 (1966) pp. 21–71 " Topology , 5 (1966) pp. 21–71 |
| [9] | A. Dold, "Halbexakte Homotopiefunktoren" , Springer (1966) |
| [10] | D. Husemoller, "Fibre bundles" , McGraw-Hill (1966) |
| [11] | R.E. Stong, "Notes on cobordism theory" , Princeton Univ. Press (1968) |
| [12] | S.P. Novikov, "The methods of algebraic topology from the view point of cobordism theories" Math. USSR-Izv. , 4 : 1 (1967) pp. 827–913 Izv. AKad. Nauk SSSR Ser. Mat. , 31 : 4 (1967) pp. 855–951 |
| [13] | J.F. Adams, "On the non-existence of elements of Hopf invariant one" Ann. of Math. , 72 (1960) pp. 20–104 |
Hopf invariant. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hopf_invariant&oldid=11380