Homothety
A transformation of Euclidean space with respect to a certain point  that brings each point
that brings each point  in a one-to-one correspondence with a point
in a one-to-one correspondence with a point  on the straight line
on the straight line  in accordance with the rule
in accordance with the rule
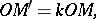 |
where  is a constant number, not equal to zero, which is known as the homothety ratio. The point
is a constant number, not equal to zero, which is known as the homothety ratio. The point  is said to be the centre of the homothety. If
is said to be the centre of the homothety. If  , the points
, the points  and
and 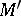 lie on the same ray; if
lie on the same ray; if  , on different sides from the centre. The point
, on different sides from the centre. The point  corresponds to itself. A homothety is a special case of a similarity. Two figures called homothetic (similar or similarly situated) if each one consists of points obtained from the other figure by a homothety with respect to some centre.
corresponds to itself. A homothety is a special case of a similarity. Two figures called homothetic (similar or similarly situated) if each one consists of points obtained from the other figure by a homothety with respect to some centre.
Simplest properties of a homothety. A homothety with  is a one-to-one mapping of the Euclidean space onto itself, with one fixed point. If
is a one-to-one mapping of the Euclidean space onto itself, with one fixed point. If  , the homothety is the identity transformation. A homothety maps a straight line (a plane) passing through its centre into itself; a straight line (a plane) not passing through its centre into a straight line (a plane) parallel to it; the angles between straight lines (planes) are preserved under this transformation. Under a homothety segments are mapped into parallel segments with a length which is
, the homothety is the identity transformation. A homothety maps a straight line (a plane) passing through its centre into itself; a straight line (a plane) not passing through its centre into a straight line (a plane) parallel to it; the angles between straight lines (planes) are preserved under this transformation. Under a homothety segments are mapped into parallel segments with a length which is  times the original length, i.e. a homothety is a contraction (expansion) of the Euclidean space at the point
times the original length, i.e. a homothety is a contraction (expansion) of the Euclidean space at the point  . Under a homothety a sphere is mapped into another sphere, and the centre of the former is mapped to the centre of the latter.
. Under a homothety a sphere is mapped into another sphere, and the centre of the former is mapped to the centre of the latter.
A homothety is most often specified (geometrically) by the homothety centre and a pair of corresponding points or by two pairs of corresponding points. A homothety is an affine transformation with one (and only one) fixed point.
In  -dimensional Euclidean space a homothety leaves the set of all
-dimensional Euclidean space a homothety leaves the set of all 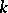 -dimensional subspaces invariant,
-dimensional subspaces invariant,  .
.
A homothety is defined in a similar manner in pseudo-Euclidean spaces. A homothety in Riemannian spaces and in pseudo-Riemannian spaces is defined as a transformation that transforms the metric of the space into itself, up to a constant factor. The set of homotheties forms a Lie group of transformations, and the  -parameter homothety group of a Riemannian space contains the
-parameter homothety group of a Riemannian space contains the  -parameter normal subgroup of displacements.
-parameter normal subgroup of displacements.
Comments
A homotopy is also called a central dilatation (cf. also Dilatation).
References
| [a1] | M. Berger, "Geometry" , 1–2 , Springer (1987) (Translated from French) |
| [a2] | H.S.M. Coxeter, "Introduction to geometry" , Wiley (1961) |
| [a3] | E. Artin, "Geometric algebra" , Interscience (1957) |
Homothety. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Homothety&oldid=11584