Homological dimension
A numerical characteristic of an object in a category with respect to a certain specified class of objects in this category. The categories of modules over a ring form the principal range of application of this concept.
Let 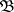 be a fixed class of objects in an Abelian category
be a fixed class of objects in an Abelian category 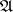 , and let
, and let  be an object in
be an object in 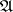 . The (projective) homological dimension of
. The (projective) homological dimension of 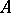 with respect to
with respect to 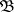 is then defined as the least number
is then defined as the least number  for which there exists an exact sequence of the form
for which there exists an exact sequence of the form
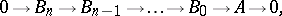 |
where all 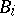 are from
are from 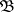 . If such an
. If such an  does not exist, one says that the homological dimension of
does not exist, one says that the homological dimension of 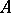 is equal to
is equal to 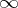 .
.
Let  (respectively,
(respectively, 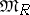 ) be the category of left (respectively, right) modules over an associative ring
) be the category of left (respectively, right) modules over an associative ring 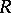 with a unit element. Then: a) if
with a unit element. Then: a) if  is the class of all projective left
is the class of all projective left 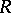 -modules, then the corresponding homological dimension of
-modules, then the corresponding homological dimension of 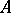 is also called the projective dimension and is denoted by
is also called the projective dimension and is denoted by 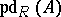 ; b) if
; b) if 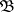 is the class of all flat left
is the class of all flat left 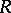 -modules, then the corresponding homological dimension of
-modules, then the corresponding homological dimension of 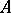 is called the weak dimension and is denoted by
is called the weak dimension and is denoted by 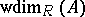 . If
. If 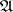 is the category of left graded modules (cf. Graded module) over a graded ring
is the category of left graded modules (cf. Graded module) over a graded ring 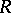 and
and 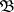 is the class of all left projective graded
is the class of all left projective graded 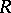 -modules, then the corresponding homological dimension of a graded
-modules, then the corresponding homological dimension of a graded  -module
-module  is called the graded projective dimension and is denoted by
is called the graded projective dimension and is denoted by 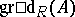 .
.
A dual construction may also be considered. If 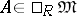 , then the least number
, then the least number  such that there exists an exact sequence
such that there exists an exact sequence
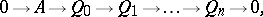 |
where all the modules  are injective, is said to be the injective dimension of
are injective, is said to be the injective dimension of 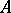 and is denoted by
and is denoted by 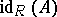 .
.
For 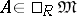 the following conditions are equivalent:
the following conditions are equivalent:
a) 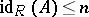 ;
;
b)  for all
for all 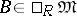 (cf. Functor Ext);
(cf. Functor Ext);
b') 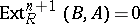 for all cyclic modules
for all cyclic modules 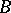 ;
;
c) 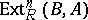 is a right-exact functor of the argument
is a right-exact functor of the argument  ;
;
d) if
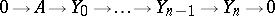 |
is an exact sequence and if the modules 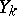 are injective for
are injective for 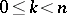 , then
, then 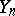 is an injective module.
is an injective module.
The following conditions are also equivalent:
a) 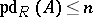 ;
;
b) 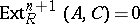 for all
for all 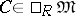 ;
;
c) 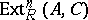 is a right-exact functor of the argument
is a right-exact functor of the argument 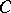 ;
;
d) if
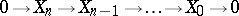 |
is an exact sequence and if the modules 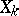 are projective for
are projective for 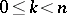 , then
, then 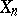 is a projective module.
is a projective module.
If the sequence
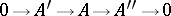 |
is exact, where 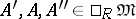 , and if
, and if
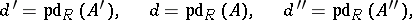 |
then
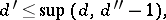 |
 |
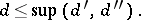 |
If 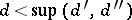 , then
, then 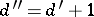 .
.
The number
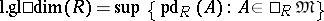 |
is called the left global dimension of the ring 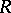 .
.
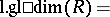 |
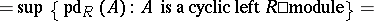 |
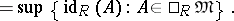 |
If the ring 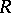 has a composition series of left ideals, then
has a composition series of left ideals, then
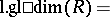 |
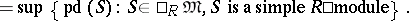 |
The number
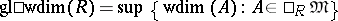 |
is called the global weak dimension of the ring 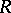 , and
, and
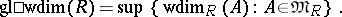 |
The number
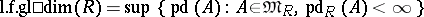 |
is called the left bounded global dimension of the ring  .
.
The following dimensions are close to these. If 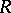 is an algebra over a commutative ring
is an algebra over a commutative ring 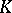 , the projective dimension of the
, the projective dimension of the  -bimodule of
-bimodule of 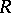 (i.e. of the left module
(i.e. of the left module 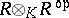 , where
, where  is the opposite ring to
is the opposite ring to 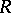 ) is called the bidimension of the algebra
) is called the bidimension of the algebra 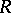 and is denoted by
and is denoted by 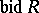 ; if
; if  is a group, and
is a group, and 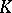 is a commutative ring, then the (co) homological dimension of the group
is a commutative ring, then the (co) homological dimension of the group 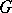 is by definition the flat (projective) dimension of the module
is by definition the flat (projective) dimension of the module 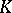 over the group ring
over the group ring 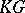 with the trivial action of
with the trivial action of 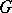 on
on 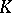 and is denoted by
and is denoted by 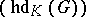
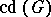 .
.
A number of well-known theorems can be reformulated in terms of the homological dimension. Thus, the Wedderburn–Artin theorem has the following form: A ring 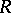 is classically simple if and only if
is classically simple if and only if 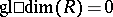 . A ring
. A ring 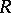 is regular in the sense of von Neumann if and only if
is regular in the sense of von Neumann if and only if 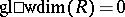 . The equality
. The equality 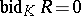 for an algebra
for an algebra 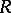 over a field
over a field 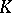 is equivalent to its separability over
is equivalent to its separability over 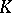 . The statement that a subgroup of a free Abelian group is free is equivalent to saying that
. The statement that a subgroup of a free Abelian group is free is equivalent to saying that 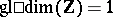 , where
, where 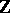 is the ring of integers. A ring
is the ring of integers. A ring 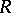 for which
for which 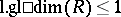 is called a left hereditary ring.
is called a left hereditary ring.
The left and right global dimensions of a ring 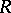 need not coincide. If, on the other hand,
need not coincide. If, on the other hand,  is both left and right Noetherian, then
is both left and right Noetherian, then
 |
If  is a ring homomorphism, then any
is a ring homomorphism, then any 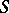 -module
-module 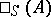 can also be regarded as an
can also be regarded as an 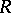 -module, and
-module, and
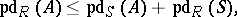 |
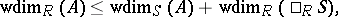 |
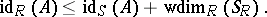 |
If the ring  is filtered, then
is filtered, then
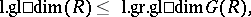 |
where 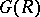 is the associated graded ring.
is the associated graded ring.
In several cases the study of homological dimensions is related to the cardinality of the modules under consideration. This makes it possible, in particular, to estimate the difference between the weak and projective dimensions of a module, and also between the left and right global dimensions of the ring. The continuum hypothesis is equivalent to
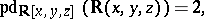 |
where 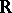 is the field of real numbers,
is the field of real numbers, 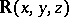 is the field of rational functions and
is the field of rational functions and 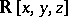 is the ring of polynomials over
is the ring of polynomials over 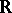 .
.
The majority of studies on homological dimensions is concerned with discovering relations between these dimensions and other characteristics of modules and fields. Thus, according to Hilbert's syzygies theorem (cf. Hilbert theorem),
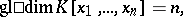 |
where 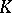 is a field and
is a field and 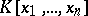 is the ring of polynomials in the variables
is the ring of polynomials in the variables  over
over  . By now this theorem has been considerably generalized. The homological dimension of group algebras of solvable groups is closely connected with the length of the solvable series of the group and with the ranks of its factors. The equation
. By now this theorem has been considerably generalized. The homological dimension of group algebras of solvable groups is closely connected with the length of the solvable series of the group and with the ranks of its factors. The equation 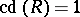 implies that
implies that 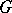 is a free group (Stallings' theorem). Another subject studied are the connections between homological dimensions and other dimensions of modules and rings. E.g., the Krull dimension of a commutative ring
is a free group (Stallings' theorem). Another subject studied are the connections between homological dimensions and other dimensions of modules and rings. E.g., the Krull dimension of a commutative ring 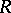 coincides with
coincides with 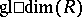 if and only if all localizations of
if and only if all localizations of 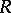 by prime ideals have finite Krull dimension. Any commutative Noetherian ring
by prime ideals have finite Krull dimension. Any commutative Noetherian ring 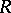 for which
for which 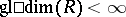 is decomposable into a finite direct sum of integral domains. The local ring of a regular point is called a regular local ring in algebraic geometry. The global dimension of such a ring is identical with its Krull dimension, and also with the minimal number of generators of its maximal ideal (regular local rings are integral domains with unique prime factorization; they remain regular after localization at prime ideals).
is decomposable into a finite direct sum of integral domains. The local ring of a regular point is called a regular local ring in algebraic geometry. The global dimension of such a ring is identical with its Krull dimension, and also with the minimal number of generators of its maximal ideal (regular local rings are integral domains with unique prime factorization; they remain regular after localization at prime ideals).
References
| [1] | H. Cartan, S. Eilenberg, "Homological algebra" , Princeton Univ. Press (1956) |
| [2] | B.L. Osofsky, "Homological dimensions of modules" , Amer. Math. Soc. (1973) |
Comments
For other dimensions of rings see (the editorial comments to) Dimension. Other notations for the projective and injective dimensions include projdim, pdim, injdim, idim.
References
| [a1] | C. Năstăsecu, F. van Oystaeyen, "Dimensions of rings" , Reidel (1988) |
Homological dimension. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Homological_dimension&oldid=16089