Hilbert space with an indefinite metric
A Hilbert space 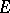 over the field of complex numbers endowed with a continuous bilinear (more exactly, sesquilinear) form
over the field of complex numbers endowed with a continuous bilinear (more exactly, sesquilinear) form 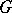 that is not, generally speaking, positive definite. The form
that is not, generally speaking, positive definite. The form 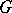 is often referred to as the
is often referred to as the 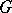 -metric. The most important example of a Hilbert space with an indefinite metric is a so-called
-metric. The most important example of a Hilbert space with an indefinite metric is a so-called 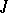 -space — a Hilbert space with an indefinite metric in which
-space — a Hilbert space with an indefinite metric in which 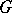 is defined by a certain Hermitian involution
is defined by a certain Hermitian involution 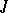 in
in 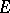 by the formula
by the formula 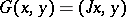 . The form
. The form 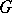 is then also denoted by the letter
is then also denoted by the letter 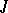 and is called a
and is called a 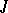 -metric. The involution
-metric. The involution 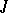 may be represented as
may be represented as 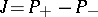 , where
, where 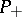 and
and 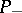 are orthogonal projections in
are orthogonal projections in 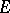 , and
, and 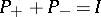 ; the number
; the number 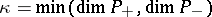 is called the rank of indefiniteness of the
is called the rank of indefiniteness of the 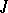 -metric or of the
-metric or of the 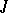 -space. If
-space. If 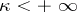 , the Hilbert space with the indefinite metric
, the Hilbert space with the indefinite metric 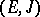 is called a Pontryagin space
is called a Pontryagin space 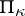 ; see also Space with an indefinite metric.
; see also Space with an indefinite metric.
Two Hilbert spaces 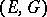 and
and 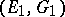 with indefinite metrics are said to be metrically equivalent if there exists a linear homeomorphism
with indefinite metrics are said to be metrically equivalent if there exists a linear homeomorphism 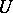 of
of 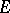 onto
onto 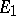 which transforms
which transforms  to
to 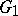 . A
. A 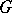 -metric generated by an invertible Hermitian operator
-metric generated by an invertible Hermitian operator 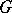 by the formula
by the formula 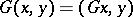 is said to be regular; after the introduction of a new scalar product that is metrically equivalent to the old one a regular
is said to be regular; after the introduction of a new scalar product that is metrically equivalent to the old one a regular 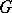 -metric becomes a
-metric becomes a 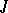 -metric. Any Hilbert space with an indefinite metric with a Hermitian form
-metric. Any Hilbert space with an indefinite metric with a Hermitian form 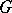 may be
may be  -isometrically (i.e. with preservation of
-isometrically (i.e. with preservation of 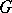 ) imbedded in some
) imbedded in some 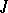 -space [2], [3].
-space [2], [3].
The principal trends in the theory of Hilbert spaces with an indefinite metric are the same as those in general spaces with an indefinite metric, but with a considerable stress on the spectral theory. The geometry of Hilbert spaces with an indefinite metric is much richer than that of ordinary spaces with an indefinite metric. Thus, in the case of 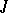 -spaces there is an effective description of the maximal subspaces
-spaces there is an effective description of the maximal subspaces  among all the non-negative (non-positive, neutral) ones: these are the
among all the non-negative (non-positive, neutral) ones: these are the 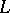 's for which
's for which 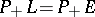 (or, correspondingly,
(or, correspondingly, 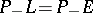 ; at least one of these equalities must be valid). Hence the analogue of the law of inertia of quadratic forms: If
; at least one of these equalities must be valid). Hence the analogue of the law of inertia of quadratic forms: If 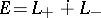 is the canonical decomposition of the
is the canonical decomposition of the 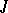 -space into a sum of semi-definite subspaces, then
-space into a sum of semi-definite subspaces, then 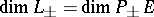 . The subspace
. The subspace 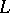 is maximal and non-negative if and only if
is maximal and non-negative if and only if 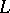 has an angular operator
has an angular operator 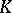 with respect to
with respect to 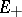 , i.e. if
, i.e. if 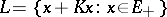 and
and 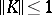 .
.
A theory of bases has been developed in 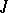 -spaces; this theory helps in the study of the geometry of Hilbert spaces with an indefinite metric as well as of the operators on them. A
-spaces; this theory helps in the study of the geometry of Hilbert spaces with an indefinite metric as well as of the operators on them. A 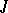 -orthonormal basis of a
-orthonormal basis of a 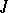 -space
-space 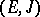 is a basis in the Hilbert space
is a basis in the Hilbert space 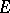 satisfying the conditions
satisfying the conditions 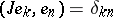 ;
; 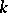 ,
, 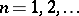 . For a
. For a 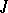 -orthonormal sequence
-orthonormal sequence 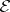 to be a Riesz basis of
to be a Riesz basis of 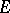 it is necessary and sufficient that
it is necessary and sufficient that 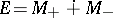 , where
, where 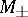 is the closed linear hull of the vectors
is the closed linear hull of the vectors 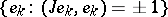 . If
. If  is a
is a  -orthonormal basis in
-orthonormal basis in 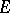 , then the decomposition
, then the decomposition 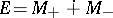 is the canonical decomposition of the
is the canonical decomposition of the 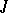 -space
-space 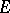 . A large group of geometrical problems in Hilbert spaces with an indefinite metric are connected with the structure and properties of so-called dual pairs of subspaces of a Hilbert space with an indefinite metric
. A large group of geometrical problems in Hilbert spaces with an indefinite metric are connected with the structure and properties of so-called dual pairs of subspaces of a Hilbert space with an indefinite metric 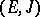 , i.e. with pairs
, i.e. with pairs  of subspaces in
of subspaces in 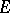 such that
such that 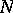 and
and 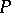 are mutually orthogonal, while
are mutually orthogonal, while  is a non-positive and
is a non-positive and  is a non-negative space. A dual pair is said to be maximal if
is a non-negative space. A dual pair is said to be maximal if  and
and 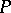 are maximal semi-definite subspaces.
are maximal semi-definite subspaces.
Theory of operators in a Hilbert space with an indefinite metric.
The metric 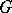 is considered to be Hermitian and non-degenerate, while the operators that are considered are densely defined. For an operator
is considered to be Hermitian and non-degenerate, while the operators that are considered are densely defined. For an operator  with domain of definition
with domain of definition 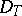 let there be defined a
let there be defined a 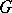 -adjoint operator
-adjoint operator 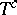 by the equation
by the equation
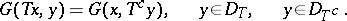 |
where 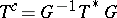 and
and
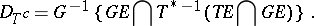 |
An operator 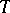 is said to be
is said to be 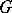 -self-adjoint if
-self-adjoint if 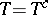 , and is said to be
, and is said to be 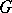 -symmetric if
-symmetric if 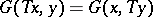 ,
, 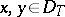 . Root subspaces
. Root subspaces 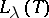 and
and 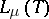 ,
, 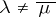 , of a
, of a 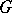 -symmetric operator
-symmetric operator 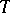 are
are 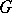 -orthogonal; in particular, if
-orthogonal; in particular, if 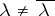 , then
, then 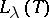 is a neutral subspace.
is a neutral subspace.
If 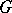 is a regular metric, then the spectrum
is a regular metric, then the spectrum 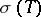 of the
of the 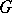 -self-adjoint operator
-self-adjoint operator 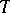 is symmetric with respect to the real axis; if it is not regular, this is usually not the case. The
is symmetric with respect to the real axis; if it is not regular, this is usually not the case. The 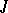 -self-adjointness of an operator
-self-adjointness of an operator 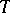 is equivalent to the self-adjointness of
is equivalent to the self-adjointness of 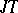 . If
. If 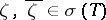 , then the Cayley transform
, then the Cayley transform 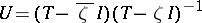 is a
is a 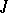 -unitary operator, i.e. is such that
-unitary operator, i.e. is such that 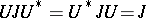 . The spectrum of
. The spectrum of 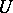 is symmetric with respect to the circle
is symmetric with respect to the circle 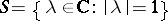 .
.
Beginning with the study of L.S. Pontryagin [1], the principal problem of the theory is the existence of semi-definite invariant subspaces. Let 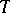 be a bounded operator in a
be a bounded operator in a  -space
-space 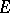 and let
and let 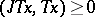 for
for 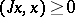 ,
,  (the so-called plus-operator); if
(the so-called plus-operator); if 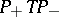 is a completely-continuous operator, then there exists a maximal non-negative
is a completely-continuous operator, then there exists a maximal non-negative 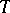 -invariant subspace
-invariant subspace 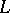 . This result is applicable, in particular, to
. This result is applicable, in particular, to 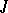 -unitary operators
-unitary operators 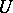 on the spaces
on the spaces 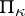 , in which it is the base of the so-called definization method — a construction of an operator polynomial
, in which it is the base of the so-called definization method — a construction of an operator polynomial 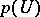 that maps
that maps 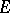 into a semi-definite subspace. This method makes it possible to obtain, e.g., analogues of the ordinary spectral expansion for
into a semi-definite subspace. This method makes it possible to obtain, e.g., analogues of the ordinary spectral expansion for 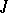 -unitary and
-unitary and 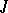 -self-adjoint operators on
-self-adjoint operators on 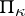 .
.
The theory of operators in Hilbert spaces with an indefinite metric is used in an essential way in the theory of canonical systems of ordinary differential equations; for example, the criterion of stability for such equations may be written as follows in terms of the monodromy operator 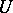 : Stability holds if and only if a maximal
: Stability holds if and only if a maximal 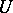 -invariant dual pair of subspaces exists. Another important use of this theory is in the spectral theory of quadratic operator pencils, which is important in many problems of mathematical physics.
-invariant dual pair of subspaces exists. Another important use of this theory is in the spectral theory of quadratic operator pencils, which is important in many problems of mathematical physics.
For the theory of representations in Hilbert spaces with an indefinite metric see [4].
References
| [1] | L.S. Pontragin, "Hermitian operators in spaces with an indefinite metric" Izv. Akad. Nauk SSR Ser. Mat. , 8 (1944) pp. 243–280 (In Russian) (English abstract) |
| [2] | Yu.P. Ginzburg, I.S. Iokhvidov, "Investigations in the geometry of infinite-dimensional spaces with a bilinear metric" Russian Math. Surveys , 17 : 4 (1962) pp. 1–51 Uspekhi Mat. Nauk , 17 : 4 (1962) pp. 3–56 |
| [3] | T.Ya. Azizov, I.S. Iokhvidov, "Linear operators in Hilbert spaces with a 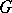 -metric" Russian Math. Surveys , 26 : 4 (1971) pp. 45–97 Uspekhi Mat. Nauk , 26 : 4 (1971) pp. 43–92 -metric" Russian Math. Surveys , 26 : 4 (1971) pp. 45–97 Uspekhi Mat. Nauk , 26 : 4 (1971) pp. 43–92 |
| [4] | M.A. Naimark, R.S. Ismagilov, "Representations of groups and algebras in spaces with an indefinite metric" Itogi Nauk. Mat. Anal. (1969) pp. 73–105 (In Russian) |
| [5] | , Functional analysis , Moscow (1964) (In Russian) |
Comments
Let 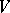 be a vector space over the complex numbers
be a vector space over the complex numbers 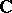 . A sesquilinear form on
. A sesquilinear form on 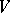 is a complex-valued function
is a complex-valued function 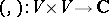 such that
such that
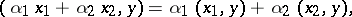 | (a1) |
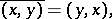 | (a2) |
for all 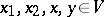 ;
; 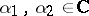 . Here the bar denotes complex conjugation. A vector space
. Here the bar denotes complex conjugation. A vector space 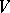 provided with such a form is called an inner product space. In an inner product space one distinguishes positive, negative and neutral elements, defined, respectively, by the conditions
provided with such a form is called an inner product space. In an inner product space one distinguishes positive, negative and neutral elements, defined, respectively, by the conditions 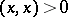 ,
, 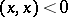 ,
, 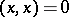 . An indefinite inner product space is one which has both positive and negative elements.
. An indefinite inner product space is one which has both positive and negative elements.
The isotropic vectors of an inner product space 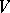 are the elements of
are the elements of 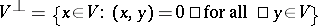 . The subspace
. The subspace  is called the isotropic part of
is called the isotropic part of 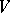 . An inner product space is non-degenerate if its isotropic part is zero.
. An inner product space is non-degenerate if its isotropic part is zero.
An inner product space is decomposable if it can be represented as an orthogonal direct sum
 | (a3) |
with 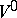 consisting of neutral elements;
consisting of neutral elements; 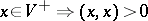 or
or 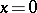 ;
; 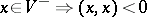 or
or 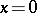 . The space
. The space 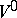 is then necessarily the isotropic part of
is then necessarily the isotropic part of 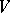 . Not every inner product space is decomposable, but every finite-dimensional one is decomposable. Every decomposition such as (a3) is called a fundamental decomposition.
. Not every inner product space is decomposable, but every finite-dimensional one is decomposable. Every decomposition such as (a3) is called a fundamental decomposition.
A definite subspace of 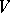 is a subspace
is a subspace 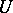 such that the restriction of
such that the restriction of 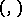 to
to 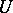 is either positive definite or negative definite. On such a subspace
is either positive definite or negative definite. On such a subspace 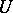 , the function
, the function  defines a norm. A definite subspace
defines a norm. A definite subspace 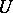 is called intrinsically complete if it is complete in the topology defined by this norm.
is called intrinsically complete if it is complete in the topology defined by this norm.
A Krein space is a non-degenerate inner product space that admits a fundamental decomposition
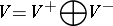 | (a4) |
such that both  and
and 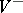 are intrinsically complete (and then that is the case for every fundamental decomposition).
are intrinsically complete (and then that is the case for every fundamental decomposition).
These are the most important types of inner product spaces. A Pontryagin space is a special kind of Krein space, viz. a Krein space for which the dimension of one of the two components in a fundamental decomposition (a4) is equal to  (and then that is the case for every fundamental decomposition).
(and then that is the case for every fundamental decomposition).
For the geometry and operator theory of Krein spaces cf. Krein space and [a1]–[a5]. For applications cf., e.g., [a6]–[a8].
The phrase "inner product space" is also used in the more restricted sense of a vector space  equipped with a sesquilinear form such that besides (a1) and (a2) also the conditions (a5) and (a6) below hold.
equipped with a sesquilinear form such that besides (a1) and (a2) also the conditions (a5) and (a6) below hold.
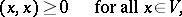 | (a5) |
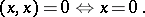 | (a6) |
I.e. in the sense of a pre-Hilbert space. In case the sesquilinear form only satisfies (a1), (a2), (a5) the phrase "pre-inner product" is used. A space with a sesquilinear form such that (a1) and (a2) hold is then called an indefinite inner product space [a8]. Thus, a partial dictionary between [a1] and [a8] is: inner product — indefinite inner product; positive semi-definite inner product — pre-inner product; positive definite inner product — inner product.
Finally, the phrases "inner product" and "inner product space" are used in still another different meaning in the theory of quadratic forms in algebra and number theory, [a9]. In that setting an inner product on a module 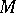 over a commutative ring
over a commutative ring 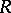 with unit is a bilinear mapping
with unit is a bilinear mapping
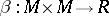 |
such that the following strong non-degeneracy conditions are satisfied: the two homomorphisms 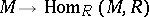 given by
given by 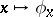 ,
, 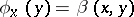 ,
, 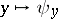 ,
, 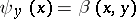 are bijective. An inner product module is then a module provided with an inner product, and an inner product space is an inner product module
are bijective. An inner product module is then a module provided with an inner product, and an inner product space is an inner product module 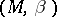 such that
such that 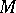 is a projective module.
is a projective module.
In turn, [a8], in the theory of Banach algebras an inner product module refers to a module 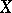 over a
over a 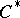 -algebra
-algebra 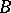 , provided with a mapping
, provided with a mapping 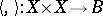 such that
such that
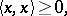 | (a7) |
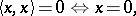 | (a8) |
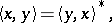 | (a9) |
 | (a10) |
for all 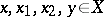 ;
; 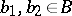 . Here
. Here 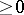 in the
in the 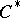 -algebra
-algebra 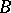 is defined as usual: An element
is defined as usual: An element 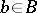 is
is 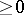 if it is Hermitian (i.e.
if it is Hermitian (i.e. 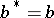 ) and of the form
) and of the form 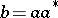 for some
for some 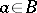 .
.
References
| [a1] | J. Bognár, "Indefinite inner product spaces" , Springer (1974) |
| [a2] | I.S. [I.S. Iokhvidov] Iohidov, M.G. Krein, H. Langer, "Introduction to the spectral theory of operators in spaces with an indefinite metric" , Akademie Verlag (1982) |
| [a3] | I. [I. Gokhberg] Gohberg, P. Lancaster, L. Rodman, "Matrices and indefinite scalar products" , Birkhäuser (1983) |
| [a4] | I.S. Iokhvidov, M.G. Krein, "Spectral theory of operators in spaces with an indefinite metric I" Transl. Amer. Math. Soc. (2) , 13 (1960) pp. 105–176 Trudy Moskov. Mat. Obshch. , 5 (1956) pp. 367–432 |
| [a5] | I.S. Iokhvidov, M.G. Krein, "Spectral theory of operators in spaces with an indefinite metric II" Transl. Amer. Math. Soc. (2) , 34 (1963) pp. 283–374 Trudy Moskov. Mat. Obshch. , 8 (1959) pp. 413–496 |
| [a6] | Yu.L. Daletskii, M.G. Krein, "Stability of solutions of differential equations in Banach space" , Amer. Math. Soc. (1974) (Translated from Russian) |
| [a7] | L. Bracci, G. Morchio, F. Strocchi, "Wigner's theorem on symmetries in indefinite metric spaces" Comm. Math. Phys. , 41 (1975) pp. 289–299 |
| [a8] | V.I. Istrăţescu, "Inner product structures" , Reidel (1987) |
| [a9] | J. Milnor, D. Husemoller, "Symmetric bilinear forms" , Springer (1973) pp. 16 |
| [a10] | T.Ya. Azizov, I.S. Iokhvidov, "Linear operators in spaces with indefinite metric and their applications" J. Soviet Math. , 15 (1981) pp. 438–490 Itogi Nauk. i Tekhn. Mat. Anal. , 17 : 4 (1979) pp. 113–205 |
Hilbert space with an indefinite metric. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hilbert_space_with_an_indefinite_metric&oldid=17153