Henselization of a valued field
A minimal algebraic extension 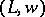 of a valued field
of a valued field 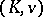 (i.e., a field
(i.e., a field 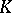 equipped with a valuation
equipped with a valuation  ) such that the valuation ring of
) such that the valuation ring of 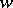 satisfies the Hensel lemma. This holds if and only if
satisfies the Hensel lemma. This holds if and only if  admits a unique extension to every algebraic extension field of
admits a unique extension to every algebraic extension field of 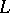 (cf. [a2]). Therefore, Henselizations can be characterized as the decomposition fields of the extensions
(cf. [a2]). Therefore, Henselizations can be characterized as the decomposition fields of the extensions 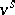 of
of  to the separable-algebraic closure
to the separable-algebraic closure 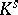 of
of 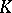 (see Ramification theory of valued fields). The minimality is expressed by the following universal property of Henselizations: they admit a unique embedding over
(see Ramification theory of valued fields). The minimality is expressed by the following universal property of Henselizations: they admit a unique embedding over  in every other Henselian extension field of
in every other Henselian extension field of 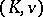 (cf. [a2]). In particular, the Henselization of
(cf. [a2]). In particular, the Henselization of 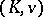 is unique up to a valuation-preserving isomorphism over
is unique up to a valuation-preserving isomorphism over 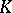 ; thus, it makes sense to denote it by
; thus, it makes sense to denote it by 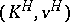 (there are some other notations in the literature). The extension
(there are some other notations in the literature). The extension 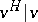 is immediate (see also valuation); for an elegant proof, see [a1].
is immediate (see also valuation); for an elegant proof, see [a1].
References
| [a1] | J. Ax, "A metamathematical approach to some problems in number theory, Appendix" D.J. Lewis (ed.) , Proc. Symp. Pure Math. , 20 , Amer. Math. Soc. (1971) pp. 161–190 |
| [a2] | P. Ribenboim, "Théorie des valuations" , Presses Univ. Montréal (1964) |
Henselization of a valued field. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Henselization_of_a_valued_field&oldid=18068