Harmonic majorant
least harmonic majorant  of a family
of a family 
The lower envelope of the family  of all superharmonic majorants
of all superharmonic majorants  of the family
of the family  of subharmonic functions on an open set
of subharmonic functions on an open set  of a Euclidean space
of a Euclidean space  ,
,  , i.e.
, i.e.
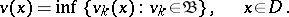 |
The least harmonic majorant  is either a harmonic function or
is either a harmonic function or 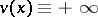 on
on  . If the family consists of a single function
. If the family consists of a single function  which is subharmonic on a larger set
which is subharmonic on a larger set  , the concept of the best harmonic majorant
, the concept of the best harmonic majorant 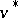 — the solution of the generalized Dirichlet problem for
— the solution of the generalized Dirichlet problem for  with value
with value  on the boundary
on the boundary 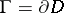 — may be employed. Always
— may be employed. Always 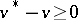 , and the following formula [1] is valid:
, and the following formula [1] is valid:
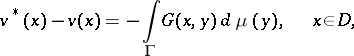 |
where 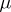 is the measure which is associated with
is the measure which is associated with  ,
, 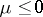 , and
, and 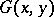 is the (generalized) Green function of the Dirichlet problem for
is the (generalized) Green function of the Dirichlet problem for 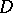 . The best and the least harmonic majorants coincide if and only if the set of all irregular points (cf. Irregular boundary point) of
. The best and the least harmonic majorants coincide if and only if the set of all irregular points (cf. Irregular boundary point) of 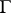 has
has  -measure zero.
-measure zero.
Correspondingly, if  is a family of superharmonic functions on
is a family of superharmonic functions on 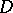 , the greatest harmonic minorant
, the greatest harmonic minorant  of the family
of the family 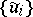 is defined as the upper envelope of the family of all subharmonic minorants of
is defined as the upper envelope of the family of all subharmonic minorants of 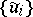 ; here
; here 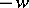 is the least harmonic majorant for
is the least harmonic majorant for  .
.
The problem of harmonic majorants may also be posed in terms of the Cauchy problem for the Laplace equation. See Harmonic function.
References
| [1] | O. Frostman, "Potentiel d'equilibre et capacité des ensembles avec quelques applications à la théorie des fonctions" Mett. Lunds Univ. Mat. Sem. , 3 (1935) pp. 1–118 |
| [2] | M. Brélot, "Eléments de la théorie classique du potentiel" , Sorbonne Univ. Centre Doc. Univ. , Paris (1959) |
Comments
In axiomatic potential theory (cf. Potential theory, abstract) the equality of the best and the least harmonic majorant is connected to the domination principle (cf. Domination), see [a1], Chapt. 9.
References
| [a1] | C. Constantinescu, A. Cornea, "Potential theory on harmonic spaces" , Springer (1972) |
Harmonic majorant. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Harmonic_majorant&oldid=15227