Hall subgroup
A subgroup of a finite group whose order is coprime to its index. It is named after Ph. Hall, who in the 1920's initiated the study of such subgroups in finite solvable groups (cf. Solvable group).
In a finite 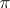 -divisible group there is a Hall
-divisible group there is a Hall 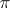 -subgroup (a Hall subgroup whose order is divisible only by the prime numbers in
-subgroup (a Hall subgroup whose order is divisible only by the prime numbers in 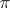 while the index is coprime to any number in
while the index is coprime to any number in 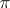 ), and all Hall
), and all Hall 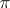 -subgroups are conjugate. A finite solvable group has a Hall
-subgroups are conjugate. A finite solvable group has a Hall 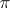 -subgroup for any set
-subgroup for any set 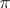 of prime numbers. Every
of prime numbers. Every  -subgroup of a finite solvable group is contained in a Hall
-subgroup of a finite solvable group is contained in a Hall 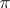 -subgroup, and all Hall
-subgroup, and all Hall 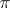 -subgroups are conjugate. A normal Hall subgroup
-subgroups are conjugate. A normal Hall subgroup 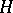 of a finite group
of a finite group 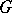 always has a complement in
always has a complement in 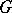 , that is, a subgroup
, that is, a subgroup 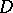 such that
such that 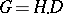 and such that
and such that 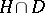 is trivial; all complements to
is trivial; all complements to 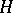 in
in 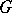 are conjugate. If a group has a nilpotent Hall
are conjugate. If a group has a nilpotent Hall 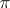 -subgroup (cf. Nilpotent group), then all Hall
-subgroup (cf. Nilpotent group), then all Hall  -subgroups are conjugate, and every
-subgroups are conjugate, and every 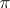 -subgroup is contained in some Hall
-subgroup is contained in some Hall 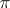 -subgroup. In general, a Hall subgroup does not have these properties. For example, the alternating group
-subgroup. In general, a Hall subgroup does not have these properties. For example, the alternating group 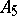 of order 60 has no Hall
of order 60 has no Hall  -subgroup. In
-subgroup. In  there is a Hall
there is a Hall  -subgroup of order 12, but there is a subgroup of order 6 which does not lie in a Hall subgroup. Finally, in the simple group of order 168 the Hall
-subgroup of order 12, but there is a subgroup of order 6 which does not lie in a Hall subgroup. Finally, in the simple group of order 168 the Hall 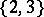 -subgroups are not conjugate.
-subgroups are not conjugate.
References
| [1] | S.A. Chunikhin, "Subgroups of finite groups" , Wolters-Noordhoff (1969) (Translated from Russian) |
| [2] | Itogi Nauk. i Tekhn. Algebra. 1964 (1966) pp. 7–46 |
| [3] | B. Huppert, "Endliche Gruppen" , 1 , Springer (1979) pp. 482–490 |
| [4] | D. Gorenstein (ed.) , Reviews on finite groups , Amer. Math. Soc. (1974) |
Hall subgroup. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hall_subgroup&oldid=18867