Hadamard theorem
Hadamard's gap theorem: If the indices 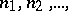 of all non-zero coefficients of the power series
of all non-zero coefficients of the power series
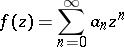 |
satisfy the condition
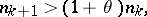 | (*) |
where 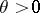 , then the boundary of the disc of convergence of this series is its natural boundary, i.e. the function has no analytic continuation across the boundary of this disc. Condition (*) is known as Hadamard's condition; the gaps which satisfy the Hadamard condition are called Hadamard gaps. See also Lacunary series; Fabry theorem.
, then the boundary of the disc of convergence of this series is its natural boundary, i.e. the function has no analytic continuation across the boundary of this disc. Condition (*) is known as Hadamard's condition; the gaps which satisfy the Hadamard condition are called Hadamard gaps. See also Lacunary series; Fabry theorem.
References
| [1] | J. Hadamard, "Essai sur l'étude des fonctions données par leurs développement de Taylor" J. Math. Pures Appl. (4) , 8 (1892) pp. 101–186 |
| [2] | L. Bieberbach, "Analytische Fortsetzung" , Springer (1955) pp. Sect. 3 |
Comments
References
| [a1] | P. Dienes, "The Taylor series" , Oxford Univ. Press (1931) |
| [a2] | G. Bourion, "L'ultraconvergence dans les séries de Taylor" , Hermann (1937) |
Hadamard's theorem on entire functions: A theorem on the representation of an entire function by means of its zeros; it makes more precise the Weierstrass theorem on infinite products in the case of an entire function 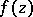 of finite order
of finite order 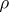 . If, for the sake of simplicity,
. If, for the sake of simplicity, 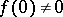 , then
, then
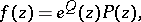 |
where  is a polynomial of degree not exceeding
is a polynomial of degree not exceeding 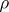 and
and
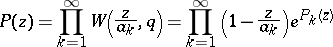 |
is Weierstrass' canonical product of genus  , constructed from the zeros
, constructed from the zeros 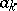 of
of 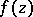 . In other words, Hadamard's theorem postulates that the genus of an entire function does not exceed its order. This theorem was used by J. Hadamard in proving an asymptotic law for the distribution of prime numbers.
. In other words, Hadamard's theorem postulates that the genus of an entire function does not exceed its order. This theorem was used by J. Hadamard in proving an asymptotic law for the distribution of prime numbers.
References
| [1] | J. Hadamard, "Étude sur les propriétés des fonctions entières et en particulier d'une fonction considérée par Riemann" J. Math. Pures Appl. (4) , 9 (1893) pp. 171–215 |
| [2] | A.I. Markushevich, "Theory of functions of a complex variable" , 1 , Chelsea (1977) (Translated from Russian) |
| [3] | B.Ya. Levin, "Distribution of zeros of entire functions" , Amer. Math. Soc. (1964) (Translated from Russian) |
Comments
References
| [a1] | R.P. Boas, "Entire functions" , Acad. Press (1954) |
| [a2] | E.C. Titchmarsh, "The theory of functions" , Oxford Univ. Press (1979) |
Hadamard's theorem on determinants: Let 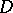 be the determinant of the matrix
be the determinant of the matrix 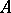 with complex entries
with complex entries  ,
, 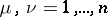 . The following inequality is then valid:
. The following inequality is then valid:
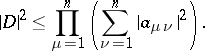 | (*) |
This inequality becomes an equality if and only if
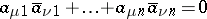 |
for each pair of different 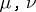 , or if at least one of the factors on the right-hand side of (*) is zero. The geometrical meaning of this theorem is that the volume of a parallelepipedon in an
, or if at least one of the factors on the right-hand side of (*) is zero. The geometrical meaning of this theorem is that the volume of a parallelepipedon in an  -dimensional space is never larger than the product of the lengths of its sides issuing from one vertex, and is equal to this product if the sides are mutually perpendicular or if the length of one of the sides is zero.
-dimensional space is never larger than the product of the lengths of its sides issuing from one vertex, and is equal to this product if the sides are mutually perpendicular or if the length of one of the sides is zero.
References
| [1] | J. Hadamard, "Résolution d'une question relative aux déterminants" Bull. Sci. Math. (2) , 17 (1893) pp. 240–246 |
O.A. Ivanova
Comments
In the special case when all entries 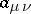 of
of 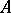 are real numbers with
are real numbers with 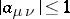 , one obtains
, one obtains 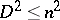 , with equality if and only if all enties are either
, with equality if and only if all enties are either 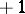 or
or 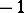 and
and 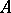 satisfies the condition
satisfies the condition 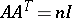 . Such a matrix is called a Hadamard matrix of order
. Such a matrix is called a Hadamard matrix of order  .
.
For references see Hadamard matrix.
Hadamard's three-circle theorem: If  is a holomorphic function of a complex variable
is a holomorphic function of a complex variable 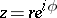 in the annulus
in the annulus 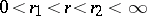 , which is continuous in the closed annulus
, which is continuous in the closed annulus 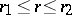 , and if
, and if 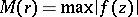 where
where  , then the following inequality is valid for
, then the following inequality is valid for 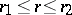 :
:
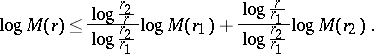 |
The meaning of this inequality is that 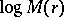 is a convex function (of a real variable) of
is a convex function (of a real variable) of 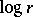 . This theorem of Hadamard is a special case of the two-constants theorem.
. This theorem of Hadamard is a special case of the two-constants theorem.
Hadamard's theorem can be generalized in various directions; in particular, there are generalizations for other metrics and for harmonic and subharmonic functions.
References
| [1] | J. Hadamard, "Sur la distribution des zéros de la fonction  et ses conséquences arithmétiques" Bull. Soc. Math. France , 24 (1896) pp. 199–220 et ses conséquences arithmétiques" Bull. Soc. Math. France , 24 (1896) pp. 199–220 |
| [2] | A.I. Markushevich, "Theory of functions of a complex variable" , 1 , Chelsea (1977) (Translated from Russian) |
| [3] | I.I. Privalov, "Subharmonic functions" , Moscow-Leningrad (1937) (In Russian) |
| [4] | E.D. Solomentsev, "A three-sphere theorem for harmonic functions" Dokl. Akad. Nauk ArmSSR , 42 : 5 (1966) pp. 274–278 (In Russian) |
Comments
References
| [a1] | R.P. Boas, "Entire functions" , Acad. Press (1954) |
| [a2] | E.C. Titchmarsh, "The theory of functions" , Oxford Univ. Press (1979) |
Hadamard's multiplication theorem (Hadamard's theorem on the multiplication of singularities): If the power series
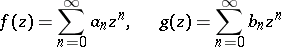 | (1) |
have convergence radii 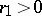 and
and 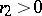 , respectively, if
, respectively, if 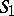 and
and 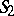 are the Mittag-Leffler stars (cf. Star of a function element) for
are the Mittag-Leffler stars (cf. Star of a function element) for 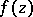 and
and 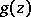 , respectively, if
, respectively, if 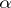 is the set of singular points of
is the set of singular points of 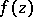 on the boundary of
on the boundary of 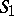 , and if
, and if  is the set of singular points of
is the set of singular points of 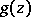 on the boundary of
on the boundary of 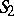 , then the power series
, then the power series
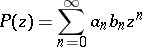 | (2) |
has radius of convergence 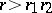 , and its Mittag-Leffler star
, and its Mittag-Leffler star 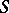 contains the star product
contains the star product 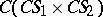 , where
, where 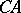 is the complement of the set
is the complement of the set 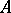 and
and 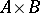 is the set of all products
is the set of all products 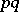 of the numbers
of the numbers 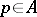 ,
, 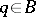 . Moreover, among the corners and readily accessible points of the boundary of the star product, only the points of the product set
. Moreover, among the corners and readily accessible points of the boundary of the star product, only the points of the product set 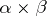 can be singular points of the function
can be singular points of the function 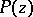 . The original statements of the theorem [1], [2] were somewhat different from the ones given above, and needed precization [2].
. The original statements of the theorem [1], [2] were somewhat different from the ones given above, and needed precization [2].
The power series (2) is known as the Hadamard product or Hadamard composition of the power series (1). The properties of the Hadamard product revealed by this theorem (and also in subsequent studies [3]) made it possible to use it in problems of analytic continuation of power series, the coefficients of the series (2) yielding some indication of the singularities of the analytic function they represent.
If 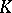 is an arbitrary compact set inside the star product
is an arbitrary compact set inside the star product 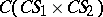 , there exists a closed rectifiable contour
, there exists a closed rectifiable contour 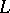 , located inside
, located inside 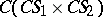 and including
and including  , such that for all
, such that for all 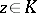 the following integral representation of the Hadamard product:
the following integral representation of the Hadamard product:
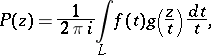 | (3) |
is valid. The representation (3) is also used in problems of analytic continuation.
References
| [1] | J. Hadamard, "Théorème sur les series entières" Acta Math. , 22 (1899) pp. 55–63 |
| [2] | J. Hadamard, "La série de Taylor et son prolongement analytique" Scientia Phys.-Math. : 12 (1901) |
| [3] | L. Bieberbach, "Analytische Fortsetzung" , Springer (1955) pp. Sect. 3 |
Comments
References
| [a1] | R.P. Boas, "Entire functions" , Acad. Press (1954) |
| [a2] | E.C. Titchmarsh, "The theory of functions" , Oxford Univ. Press (1979) |
| [a3] | C. Pommerenke, "Univalent functions" , Vandenhoeck & Ruprecht (1975) |
Hadamard theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hadamard_theorem&oldid=15608