Hadamard matrix

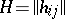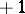A square matrix of order , with entries or 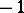, such that the equation

(*)

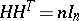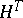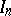holds, where is the transposed matrix of and is the unit matrix of order . Equality (*) is equivalent to saying that any two rows of 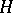are orthogonal. Hadamard matrices have been named after J. Hadamard who showed [1] that the determinant 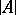of a matrix 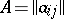of order , with complex entries, satisfies the Hadamard inequality

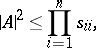where

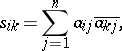and 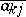is the element conjugate to 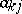(cf. Hadamard theorem on determinants). In particular, if , then 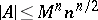. It follows that a Hadamard matrix is a square matrix consisting of 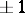's with maximal absolute value 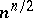of the determinant. The properties of Hadamard matrices are: 1) 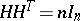implies and vice versa; 2) transposition of rows or columns and multiplication of the elements of an arbitrary row or column by 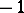again yields a Hadamard matrix; 3) the tensor product of two Hadamard matrices is also a Hadamard matrix, of order equal to the product of the orders of the factors. In other words, if 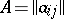and 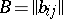are Hadamard matrices of orders 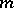and respectively, then is a Hadamard matrix of order 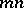. A Hadamard matrix with its first row and first column consisting only of 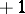terms is said to be normalized. The order of a Hadamard matrix is 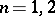or 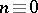(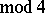). The normalized Hadamard matrices of orders 1 and 2 are:

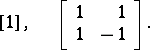The existence of a Hadamard matrix has been demonstrated for several classes of values of (see, for example, [2], [3]). At the time of writing (the 1980s), it has not yet been proved that a Hadamard matrix exists for any 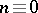(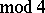). For methods of constructing Hadamard matrices see [2]. Hadamard matrices are used in the construction of certain types of block designs [2] and codes [3] (cf. Block design; Code). A Hadamard matrix of order 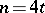is equivalent to a 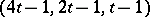-design.

A generalized Hadamard matrix is a square matrix of order 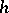, with as entries 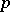-th roots of unity, which satisfies the equality

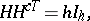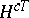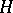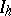where is the conjugate transpose of the matrix and is the unit matrix of order 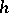. Generalized Hadamard matrices have properties analogous to 1) and 3) (cf. [4]).

References

[1]	J. Hadamard, "Résolution d'une question relative aux déterminants" Bull. Sci. Math. (2) , 17 (1893) pp. 240–246
[2]	M. Hall, "Combinatorial theory" , Blaisdell (1967) pp. Chapt. 14
[3]	W.W. Peterson, "Error-correcting codes" , M.I.T. & Wiley (1961)
[4]	A.T. Butson, "Generalized Hadamard matrices" Proc. Amer. Math. Soc. , 13 (1962) pp. 894–898

Comments

Hadamard matrices are equivalent to so-called Hadamard -designs; they are also important in statistical applications [a6].

References

[a1]	W.D. Wallis, A.P. Street, J.S. Wallis, "Combinatorics: room squares, sum-free sets, Hadamard matrices" , Springer (1972)
[a2]	D.R. Hughes, F.C. Piper, "Design theory" , Cambridge Univ. Press (1988)
[a3]	F.J. MacWilliams, N.J.A. Sloane, "The theory of error-correcting codes" , I-II , North-Holland (1977)
[a4]	S.S. Agaian, "Hadamard matrices and their applications" , Lect. notes in math. , 1168 , Springer (1985)
[a5]	T. Beth, D. Jungnickel, H. Lenz, "Design theory" , Cambridge Univ. Press (1986)
[a6]	A. Hedayat, W.D. Wallis, "Hadamard matrices and their applications" Ann. Stat. , 6 (1978) pp. 1184–1238