HNN-extension
In 1949, G. Higman, B.H. Neumann and H. Neumann [a4] proved several famous embedding theorems for groups using a construction later called the HNN-extension. The theory of HNN-groups is central to geometric and combinatorial group theory and should be viewed in parallel with amalgamated products (cf. also Amalgam of groups).
The easiest way to define an HNN-group is in terms of presentations of groups.
Presentation of groups.
A presentation of a group  is a pair
is a pair  where
where  is a subset of
is a subset of  , the free group on the set
, the free group on the set  , and
, and  is isomorphic (cf. also Isomorphism) to the quotient group
is isomorphic (cf. also Isomorphism) to the quotient group  , where
, where  is the intersection of all normal subgroups of
is the intersection of all normal subgroups of  containing
containing 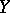 (cf. also Normal subgroup). The subgroup
(cf. also Normal subgroup). The subgroup 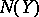 is called the normal closure of
is called the normal closure of  in
in 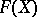 . See also Presentation.
. See also Presentation.
Given an arbitrary group 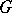 , there is an obvious homomorphism
, there is an obvious homomorphism 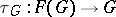 such that
such that 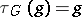 for all
for all 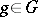 . Clearly,
. Clearly, 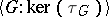 is a presentation for
is a presentation for 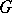 .
.
HNN-extensions.
Suppose 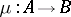 is an isomorphism of subgroups of a group
is an isomorphism of subgroups of a group 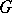 and
and 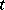 is not in
is not in 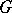 . The HNN-extension of
. The HNN-extension of  with respect to
with respect to 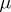 has presentation
has presentation
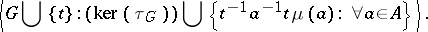 |
The generator 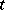 is called the stable letter,
is called the stable letter, 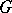 the base group and
the base group and 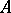 and
and 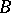 the associated subgroups of this HNN-extension. When
the associated subgroups of this HNN-extension. When 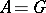 , the HNN-extension is called ascending.
, the HNN-extension is called ascending.
Shorthand notation for the above group is 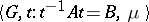 or
or 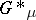 .
.
In [a4] it was shown that the mapping 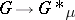 taking
taking 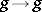 for all
for all 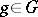 is a monomorphism. The rest of the normal form theorem for HNN-extensions was proved by J.L. Britton in 1963 [a1] (Britton's lemma): Let
is a monomorphism. The rest of the normal form theorem for HNN-extensions was proved by J.L. Britton in 1963 [a1] (Britton's lemma): Let 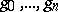 be a sequence of elements of
be a sequence of elements of 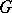 and let the letter
and let the letter  , with or without subscripts, denote
, with or without subscripts, denote 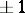 . A sequence
. A sequence 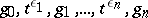 will be called reduced if there is no consecutive subsequence
will be called reduced if there is no consecutive subsequence 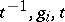 with
with 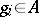 or
or 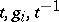 with
with 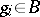 . For a reduced sequence and
. For a reduced sequence and 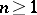 , the element
, the element
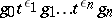 |
of 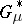 is different from the unit element.
is different from the unit element.
In the original reference [a4], the following theorem is proved: Every group 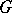 can be embedded in a group
can be embedded in a group 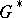 in which all elements of the same order are conjugate (cf. also Conjugate elements). In particular, every torsion-free group can be embedded in a group
in which all elements of the same order are conjugate (cf. also Conjugate elements). In particular, every torsion-free group can be embedded in a group 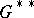 with only two conjugacy classes. If
with only two conjugacy classes. If 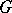 is countable, so is
is countable, so is  . Also, every countable group
. Also, every countable group  can be embedded in a group
can be embedded in a group 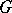 generated by two elements of infinite order. The group
generated by two elements of infinite order. The group 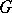 has an element of finite order
has an element of finite order  if and only if
if and only if 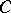 does. If
does. If  is finitely presentable, then so is
is finitely presentable, then so is 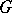 .
.
For an excellent account of the history of HNN-extensions, see [a2]. See [a5], Chap. IV, for basic results and landmark uses of HNN-extensions, such as: the torsion theorem for HNN-extensions; the Collins conjugacy theorem for HNN-extensions; the construction of finitely-presented non-Hopfian groups (in particular, the Baumslag–Solitar group 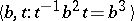 is non-Hopfian; cf. also Non-Hopf group); decompositions of
is non-Hopfian; cf. also Non-Hopf group); decompositions of  -relator groups; Stallings' classification of finitely-generated groups with more than one end in terms of amalgamated products and HNN-extensions; and Stallings' characterization of bipolar structures on groups.
-relator groups; Stallings' classification of finitely-generated groups with more than one end in terms of amalgamated products and HNN-extensions; and Stallings' characterization of bipolar structures on groups.
HNN-extensions are of central importance in, e.g., the modern version of the Van Kampen theorem (based on topological results in [a8], [a9]); the Bass–Serre theory of groups acting on trees and the theory of graphs of groups (see [a7]); Dunwoody's accessibility theorem [a3]; and JSJ decompositions of groups [a6].
References
| [a1] | J.L. Britton, "The word problem" Ann. of Math. , 77 (1963) pp. 16–32 |
| [a2] | B. Chandler, W. Magnus, "The history of combinatorial group theory: A case study in the history of ideas" , Studies History Math. and Phys. Sci. , 9 , Springer (1982) |
| [a3] | M.J. Dunwoody, "The accessibility of finitely presented groups" Invent. Math. , 81 (1985) pp. 449–457 |
| [a4] | G. Higman, B.H. Neumann, H. Neumann, "Embedding theorems for groups" J. London Math. Soc. , 24 (1949) pp. 247–254; II.4, 13 |
| [a5] | R. Lyndon, P. Schupp, "Combinatorial group theory" , Springer (1977) |
| [a6] | E. Rips, Z. Sela, "Cyclic splittings of finitely presented groups and the canonical JSJ decomposition" Ann. of Math. (2) , 146 : 1 (1997) pp. 53–109 |
| [a7] | J.P. Serre, "Arbres, amalgams,  " Astéerisque , 46 (1977) " Astéerisque , 46 (1977) |
| [a8] | E.R. Van Kampen, "On the connection between the fundamental groups of some related spaces" Amer. J. Math. , 55 (1933) pp. 261–267 |
| [a9] | E.R. Van Kampen, "On some lemmas in the theory of groups" Amer. J. Math. , 55 (1933) pp. 268–273 |
HNN-extension. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=HNN-extension&oldid=17603