Green equivalence relations
on a semi-group
Binary relations  ,
,  ,
,  ,
,  ,
,  defined as follows:
defined as follows:  means that
means that  and
and  generate identical left principal ideals (cf. Principal ideal);
generate identical left principal ideals (cf. Principal ideal);  and
and 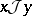 have a similar meaning after "left" has been replaced by "right" and "two-sided" , respectively;
have a similar meaning after "left" has been replaced by "right" and "two-sided" , respectively; 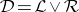 (union in the lattice of equivalence relations);
(union in the lattice of equivalence relations); 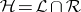 . The relations
. The relations 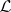 and
and  are commutative in the sense of multiplication of binary relations, so that
are commutative in the sense of multiplication of binary relations, so that  coincides with their product. The relation
coincides with their product. The relation 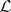 is a right congruence, i.e. is stable from the right:
is a right congruence, i.e. is stable from the right: 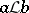 implies
implies 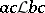 for all
for all  ; the relation
; the relation 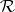 is a left congruence (stable from the left). An
is a left congruence (stable from the left). An 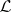 -class and an
-class and an 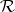 -class intersect if and only if they are contained in the same
-class intersect if and only if they are contained in the same 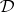 -class. All
-class. All 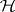 -classes in the same
-classes in the same 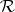 -class are equipotent. If a
-class are equipotent. If a 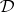 -class
-class  contains a regular element, then all elements in
contains a regular element, then all elements in 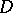 are regular and
are regular and 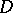 contains with some given element all elements inverse to it; such a
contains with some given element all elements inverse to it; such a 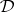 -class is said to be regular. In a regular
-class is said to be regular. In a regular 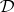 -class each
-class each 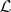 -class and each
-class and each 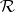 -class contains an idempotent. Let
-class contains an idempotent. Let 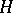 be an arbitrary
be an arbitrary 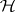 -class; then either
-class; then either 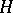 is a group (which is the case if and only if
is a group (which is the case if and only if 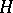 is a maximal subgroup of the given semi-group), or else
is a maximal subgroup of the given semi-group), or else 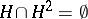 . All group
. All group 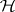 -classes of the same
-classes of the same  -class are isomorphic groups. In the general case
-class are isomorphic groups. In the general case 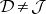 , but if, for example, some power of each element of the semi-group
, but if, for example, some power of each element of the semi-group 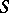 belongs to a subgroup (in particular, if
belongs to a subgroup (in particular, if 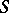 is a periodic semi-group), then
is a periodic semi-group), then  . The inclusion of principal left ideals defines in a natural manner a partial order relation on the set of
. The inclusion of principal left ideals defines in a natural manner a partial order relation on the set of 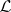 -classes; similar considerations are valid for
-classes; similar considerations are valid for 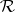 -classes and
-classes and  -classes. These relations were introduced by J. Green [1].
-classes. These relations were introduced by J. Green [1].
References
| [1] | J. Green, "On the structure of semigroups" Ann. of Math. , 54 (1951) pp. 163–172 |
| [2] | E.S. Lyapin, "Semigroups" , Amer. Math. Soc. (1974) (Translated from Russian) |
| [3] | A.H. Clifford, G.B. Preston, "Algebraic theory of semi-groups" , 1–2 , Amer. Math. Soc. (1961–1967) |
| [4] | , The algebraic theory of automata, languages and semi-groups , Moscow (1975) (In Russian; translated from English) |
| [5] | K.H. Hofmann, P.S. Mostert, "Elements of compact semigroups" , C.E. Merrill (1966) |
Green equivalence relations. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Green_equivalence_relations&oldid=16826