Greatest common divisor
The largest of the common divisors of a set of integers or, in particular, of natural numbers  . The greatest common divisor of a set of numbers not all of which are zero always exists. The greatest common divisor of
. The greatest common divisor of a set of numbers not all of which are zero always exists. The greatest common divisor of  is usually denoted by
is usually denoted by 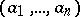 .
.
Properties of the greatest common divisor are:
1) The greatest common divisor of  is divisible by any common divisor of these numbers.
is divisible by any common divisor of these numbers.
2) 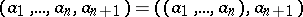 .
.
3) If  are expressed as
are expressed as
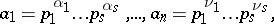 |
where 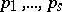 are distinct primes,
are distinct primes, 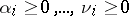 ,
, 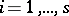 , and
, and 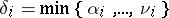 , then
, then
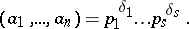 |
The greatest common divisor of two natural numbers can be determined by the Euclidean algorithm. The number of steps necessary to do this is bounded from above by five times the number of digits in the smaller of the two numbers (in decimal notation).
The greatest common divisor of elements of an integral domain is defined as the common divisor of these elements that is divisible by any other common divisor. Thus, the greatest common divisor of two polynomials over a given field is the common divisor that is divisible by any other common divisor of the polynomials. If the greatest common divisor of two elements of an integral domain exists, it is unique up to multiplication by an invertible element. The greatest common divisor of two ideals  and
and 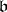 in a ring is the ideal
in a ring is the ideal 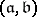 generated by the union of the sets
generated by the union of the sets  and
and 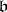 (see Factorial ring).
(see Factorial ring).
References
| [1] | I.M. Vinogradov, "Elements of number theory" , Dover, reprint (1954) (Translated from Russian) |
| [2] | A.A. Bukhshtab, "Number theory" , Moscow (1966) (In Russian) |
| [3] | A.I. Markushevich, "Division with remainder in arithmetic and algebra" , Moscow-Leningrad (1949) (In Russian) |
| [4] | R. Faure, A. Kaufman, M. Denis-Papin, "Mathématique nouvelle" , Dunod (1964) |
| [5] | S. Lang, "Algebra" , Addison-Wesley (1974) |
| [6] | K. Ireland, M. Rosen, "A classical introduction to modern number theory" , Springer (1982) |
Comments
More generally, if 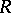 is a domain, a greatest common divisor
is a domain, a greatest common divisor 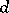 of a set
of a set 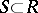 , not all
, not all 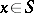 zero, is characterized by the fact that any common divisor of all
zero, is characterized by the fact that any common divisor of all 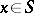 divides
divides 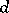 . If for any
. If for any 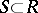 with not all
with not all 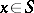 zero such a
zero such a 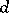 exists,
exists, 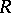 is called a principal ideal domain (cf. Principal ideal ring). Examples of such domains are the ring
is called a principal ideal domain (cf. Principal ideal ring). Examples of such domains are the ring 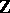 of rational integers or polynomial rings
of rational integers or polynomial rings 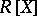 , where
, where 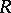 is a field (e.g.,
is a field (e.g., 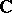 or
or 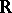 or
or 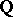 ). It is known that a principal ideal domain is also a unique factorization domain.
). It is known that a principal ideal domain is also a unique factorization domain.
References
| [a1] | B.L. van der Waerden, "Algebra" , 1 , Springer (1967) (Translated from German) |
Greatest common divisor. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Greatest_common_divisor&oldid=17623