Gradient method
From Encyclopedia of Mathematics
A method for the minimization of a function of several variables. It is based on the fact that each successive approximation of the function 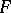 is obtained from the preceding one by a shift in the direction of the gradient of the function:
is obtained from the preceding one by a shift in the direction of the gradient of the function:
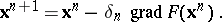 |
The parameter 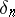 can be obtained, e.g., from the condition of the magnitude
can be obtained, e.g., from the condition of the magnitude
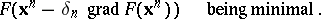 |
See also Descent, method of; Steepest descent, method of.
Comments
References
| [a1] | J.E. Dennis, R.B. Schnabel, "Numerical methods for unconstrained optimization and nonlinear equations" , Prentice-Hall (1983) MR0702023 Zbl 0579.65058 |
| [a2] | R. Fletcher, "Practical methods of optimization" , Wiley (1980) MR0585160 MR0633058 Zbl 0439.93001 |
| [a3] | D.G. Luenberger, "Linear and nonlinear programming" , Addison-Wesley (1984) MR2423726 MR2012832 Zbl 0571.90051 |
How to Cite This Entry:
Gradient method. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Gradient_method&oldid=28206
Gradient method. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Gradient_method&oldid=28206