Gradient
One of the fundamental concepts in vector analysis and the theory of non-linear mappings.
The gradient of a scalar function 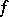 of a vector argument
of a vector argument 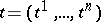 from a Euclidean space
from a Euclidean space 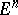 is the derivative of
is the derivative of 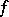 with respect to the vector argument
with respect to the vector argument 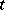 , i.e. the
, i.e. the  -dimensional vector with components
-dimensional vector with components 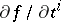 ,
, 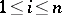 . The following notations exist for the gradient of
. The following notations exist for the gradient of 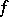 at
at 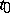 :
:
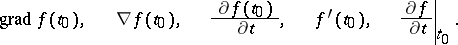 |
The gradient is a covariant vector: the components of the gradient, computed in two different coordinate systems 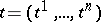 and
and 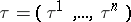 , are connected by the relations:
, are connected by the relations:
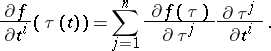 |
The vector 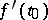 , with its origin at
, with its origin at 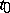 , points to the direction of fastest increase of
, points to the direction of fastest increase of 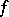 , and is orthogonal to the level lines or surfaces of
, and is orthogonal to the level lines or surfaces of 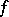 passing through
passing through 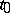 .
.
The derivative of the function at 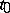 in the direction of an arbitrary unit vector
in the direction of an arbitrary unit vector 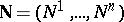 is equal to the projection of the gradient function onto this direction:
is equal to the projection of the gradient function onto this direction:
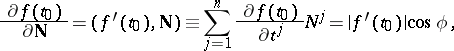 | (1) |
where 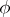 is the angle between
is the angle between 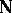 and
and 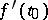 . The maximal directional derivative is attained if
. The maximal directional derivative is attained if 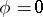 , i.e. in the direction of the gradient, and that maximum is equal to the length of the gradient.
, i.e. in the direction of the gradient, and that maximum is equal to the length of the gradient.
The concept of a gradient is closely connected with the concept of the differential of a function. If 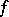 is differentiable at
is differentiable at 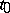 , then, in a neighbourhood of that point,
, then, in a neighbourhood of that point,
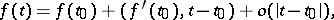 | (2) |
i.e. 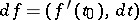 . The existence of the gradient of
. The existence of the gradient of 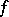 at
at 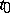 is not sufficient for formula (2) to be valid.
is not sufficient for formula (2) to be valid.
A point 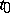 at which
at which 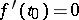 is called a stationary (critical or extremal) point of
is called a stationary (critical or extremal) point of 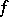 . An example of such a point is a local extremal point of
. An example of such a point is a local extremal point of 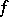 , and the system
, and the system 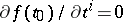 ,
, 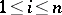 , is employed to find an extremal point
, is employed to find an extremal point  .
.
The following formulas can be used to compute the value of the gradient:
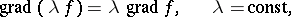 |
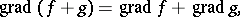 |
 |
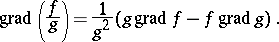 |
The gradient 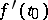 is the derivative at
is the derivative at 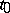 with respect to volume of the vector function given by
with respect to volume of the vector function given by
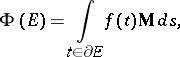 |
where 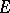 is a domain with boundary
is a domain with boundary 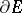 ,
, 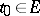 ,
, 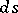 is the area element of
is the area element of 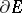 , and
, and 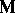 is the unit vector of the outward normal to
is the unit vector of the outward normal to 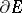 . In other words,
. In other words,
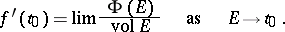 |
Formulas (1), (2) and the properties of the gradient listed above indicate that the concept of a gradient is invariant with respect to the choice of a coordinate system.
In a curvilinear coordinate system 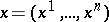 , in which the square of the linear element is
, in which the square of the linear element is
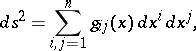 |
the components of the gradient of 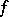 with respect to the unit vectors tangent to coordinate lines at
with respect to the unit vectors tangent to coordinate lines at  are
are
 |
where the matrix 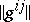 is the inverse of the matrix
is the inverse of the matrix 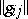 .
.
The concept of a gradient for more general vector functions of a vector argument is introduced by means of equation (2). Thus, the gradient is a linear operator the effect of which on the increment 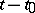 of the argument is to yield the principal linear part of the increment
of the argument is to yield the principal linear part of the increment 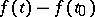 of the vector function
of the vector function 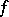 . E.g., if
. E.g., if 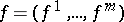 is an
is an 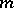 -dimensional vector function of the argument
-dimensional vector function of the argument 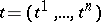 , then its gradient at a point
, then its gradient at a point 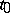 is the Jacobi matrix
is the Jacobi matrix 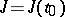 with components
with components 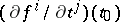 ,
, 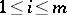 ,
, 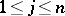 , and
, and
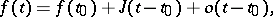 |
where 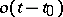 is an
is an 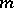 -dimensional vector of length
-dimensional vector of length 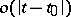 . The matrix
. The matrix 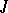 is defined by the limit transition
is defined by the limit transition
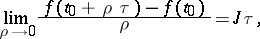 | (3) |
for any fixed  -dimensional vector
-dimensional vector  .
.
In an infinite-dimensional Hilbert space definition (3) is equivalent to the definition of differentiability according to Fréchet, the gradient then being identical with the Fréchet derivative.
If the values of 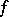 lie in an infinite-dimensional vector space, various types of limit transitions in (3) are possible (see, for example, Gâteaux derivative).
lie in an infinite-dimensional vector space, various types of limit transitions in (3) are possible (see, for example, Gâteaux derivative).
In the theory of tensor fields on a domain of an  -dimensional affine space with a connection, the gradient serves to describe the principal linear part of increment of the tensor components under parallel displacement corresponding to the connection. The gradient of a tensor field
-dimensional affine space with a connection, the gradient serves to describe the principal linear part of increment of the tensor components under parallel displacement corresponding to the connection. The gradient of a tensor field
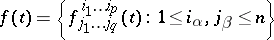 |
of type 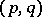 is the tensor of type
is the tensor of type 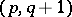 with components
with components
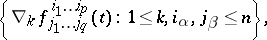 |
where 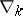 is the operator of absolute (covariant) differentiation (cf. Covariant differentiation).
is the operator of absolute (covariant) differentiation (cf. Covariant differentiation).
The concept of a gradient is widely employed in many problems in mathematics, mechanics and physics. Many physical fields can be regarded as gradient fields (cf. Potential field).
References
| [1] | N.E. Kochin, "Vector calculus and fundamentals of tensor calculus" , Moscow (1965) (In Russian) |
| [2] | P.K. [P.K. Rashevskii] Rashewski, "Riemannsche Geometrie und Tensoranalyse" , Deutsch. Verlag Wissenschaft. (1959) (Translated from Russian) |
Comments
References
| [a1] | W. Fleming, "Functions of several variables" , Addison-Wesley (1965) |
Gradient. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Gradient&oldid=28205