Germ
A term signifying a "pointwise localization" of various mathematical objects (germs of functions, germs of mappings, germs of analytic sets, etc.). Let, for example,  be a point in a topological space and let
be a point in a topological space and let 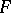 be some family of functions defined in a neighbourhood of
be some family of functions defined in a neighbourhood of  (each in its own neighbourhood). Two functions
(each in its own neighbourhood). Two functions 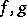 are said to be equivalent (at
are said to be equivalent (at  ) if they coincide in some neighbourhood of
) if they coincide in some neighbourhood of  . An equivalence class generated by this relation is called a germ of functions of class
. An equivalence class generated by this relation is called a germ of functions of class 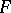 at
at  . In this way are defined the germs of continuous functions, of differentiable functions at the points of a differentiable manifold, of holomorphic functions at the points of a complex manifold, etc. If the family
. In this way are defined the germs of continuous functions, of differentiable functions at the points of a differentiable manifold, of holomorphic functions at the points of a complex manifold, etc. If the family 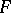 has some algebraic structure, then the set of germs of functions of the family
has some algebraic structure, then the set of germs of functions of the family 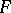 inherits this structure (the operations are carried out on representatives of classes). In particular, the germs of holomorphic functions at a point
inherits this structure (the operations are carried out on representatives of classes). In particular, the germs of holomorphic functions at a point  form a ring. Elements of the quotient field of this ring are called germs of meromorphic functions at
form a ring. Elements of the quotient field of this ring are called germs of meromorphic functions at  .
.
Similarly one can define a germ of a family of subsets of a topological space. For instance, at the points of an analytic manifold there are germs of analytic sets (the equivalence class is defined by coincidence in a neighbourhood of a given point). On germs of families of subsets set-theoretic operations and relations are naturally defined. The notion of a germ is also meaningful in the case of other objects defined on open subsets of a topological space.
See also Analytic function; Meromorphic function; Sheaf.
References
| [1] | R.C. Gunning, H. Rossi, "Analytic functions of several complex variables" , Prentice-Hall (1965) |
Comments
The germs of analytic spaces or schemes are characterized by the stalks of their structure sheaves. These are local rings.
The study of germs of differentiable mappings is the subject of singularity theory (cf. Singularities of differentiable mappings).
An important theorem for the theory of germs of analytic sets is Weierstrass' preparation theorem (cf. Weierstrass theorem), see also [a1].
References
| [a1] | M. Hervé, "Several complex variables: local theory" , Oxford Univ. Press (1967) |
Germ. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Germ&oldid=17443