Geometric genus
A numerical invariant of non-singular algebraic varieties. In the case of algebraic curves the geometric genus becomes identical with the genus of the curve (cf. Genus of a curve). The geometric genus for algebraic surfaces was first defined from different points of view by A. Clebsch and M. Noether in the second half of the 19th century. Noether also demonstrated the birational invariance of the geometric genus. The geometric genus of a non-singular projective algebraic variety 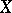 over an algebraically closed field
over an algebraically closed field 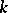 is, by definition, the dimension of the space of regular differential forms (cf. Differential form) of degree
is, by definition, the dimension of the space of regular differential forms (cf. Differential form) of degree 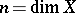 . In such a case the geometric genus of
. In such a case the geometric genus of 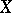 is denoted by
is denoted by 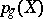 . In accordance with Serre's duality theorem
. In accordance with Serre's duality theorem
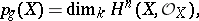 |
where 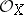 is the structure sheaf of
is the structure sheaf of 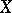 . The number
. The number 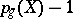 coincides with the dimension of the canonical system of
coincides with the dimension of the canonical system of 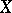 (cf. also Divisor). The geometric genus plays an important role in the criterium of rationality of algebraic surfaces (cf. Rational surface) and also in the general classification of algebraic surfaces. The geometric genera of birationally-isomorphic smooth projective varieties coincide.
(cf. also Divisor). The geometric genus plays an important role in the criterium of rationality of algebraic surfaces (cf. Rational surface) and also in the general classification of algebraic surfaces. The geometric genera of birationally-isomorphic smooth projective varieties coincide.
References
| [1] | M. Baldassarri, "Algebraic varieties" , Springer (1956) |
| [2] | I.R. Shafarevich, "Basic algebraic geometry" , Springer (1977) (Translated from Russian) |
Comments
See also Arithmetic genus.
References
| [a1] | R. Hartshorne, "Algebraic geometry" , Springer (1977) |
Geometric genus. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Geometric_genus&oldid=18019