Genus of a curve
A numerical invariant of a one-dimensional algebraic variety defined over a field  . The genus of a smooth complete algebraic curve
. The genus of a smooth complete algebraic curve  is equal to the dimension of the space of regular differential
is equal to the dimension of the space of regular differential  -forms on
-forms on  (cf. Differential form). The genus of an algebraic curve
(cf. Differential form). The genus of an algebraic curve  is equal, by definition, to the genus of the complete algebraic curve birationally isomorphic to
is equal, by definition, to the genus of the complete algebraic curve birationally isomorphic to  . For any integer
. For any integer  there exists an algebraic curve of genus
there exists an algebraic curve of genus  . An algebraic curve of genus
. An algebraic curve of genus  over an algebraically closed field is a rational curve, i.e. it is birationally isomorphic to the projective line
over an algebraically closed field is a rational curve, i.e. it is birationally isomorphic to the projective line  . Curves of genus
. Curves of genus 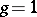 (elliptic curves, cf. Elliptic curve) are birationally isomorphic to smooth cubic curves in
(elliptic curves, cf. Elliptic curve) are birationally isomorphic to smooth cubic curves in 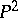 . The algebraic curves of genus
. The algebraic curves of genus 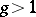 fall into two classes: hyper-elliptic curves and non-hyper-elliptic curves. For non-hyper-elliptic curves
fall into two classes: hyper-elliptic curves and non-hyper-elliptic curves. For non-hyper-elliptic curves 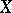 the rational mapping
the rational mapping  defined by the canonical class
defined by the canonical class 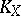 of the complete smooth curve is an isomorphic imbedding. For a hyper-elliptic curve
of the complete smooth curve is an isomorphic imbedding. For a hyper-elliptic curve 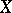 the mapping
the mapping 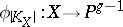 is a two-sheeted covering of a rational curve,
is a two-sheeted covering of a rational curve, 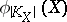 , ramified at
, ramified at 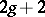 points.
points.
If 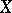 is a projective plane curve of degree
is a projective plane curve of degree 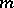 , then
, then
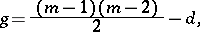 |
where 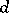 is a non-negative integer measuring the deviation from smoothness of
is a non-negative integer measuring the deviation from smoothness of 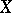 . If
. If 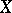 has only ordinary double points, then
has only ordinary double points, then 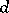 is equal to the number of singular points of
is equal to the number of singular points of 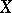 . For a curve
. For a curve  in space the following estimate is valid:
in space the following estimate is valid:
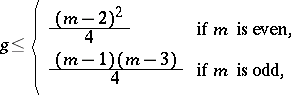 |
where 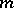 is the degree of
is the degree of 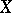 in
in 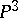 .
.
If 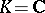 is the field of complex numbers, then an algebraic curve
is the field of complex numbers, then an algebraic curve  is the same as a Riemann surface. In this case the smooth complex curve
is the same as a Riemann surface. In this case the smooth complex curve  of genus
of genus 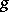 is homeomorphic to the sphere with
is homeomorphic to the sphere with  handles.
handles.
References
| [1] | I.R. Shafarevich, "Basic algebraic geometry" , Springer (1977) (Translated from Russian) |
| [2] | R. Hartshorne, "Algebraic geometry" , Springer (1977) pp. 91 |
Comments
References
| [a1] | G. Springer, "Introduction to Riemann surfaces" , Addison-Wesley (1957) pp. Chapt.10 |
| [a2] | P.A. Griffiths, J.E. Harris, "Principles of algebraic geometry" , Wiley (Interscience) (1978) |
Genus of a curve. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Genus_of_a_curve&oldid=13874