General aggregate
population
A concept in the theory of statistical sampling methods (cf. Sample method). In mathematical statistics a "general aggregate" or "population" is a set of elements of the same type out of which a certain subset — a sample — is drawn in accordance with a given rule. For instance, in statistical quality control involving the destruction of the items tested, the population is the set of items subject to general characterization (in the sense of lifetime, conformity to given norms, tolerances, etc.); in the simplest cases the control sample is drawn from the population at random. From the view of probability theory, a "random" choice means that if the population contains 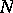 elements and the sample size is
elements and the sample size is  elements (
elements (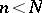 ), then the selection should be so effected that any group of
), then the selection should be so effected that any group of  elements is drawn with probability
elements is drawn with probability  . This rule of sampling is realized in determining the winning lottery tickets out of the total number of lottery tickets, considered to be the population which, on account of its nature, must necessarily be finite.
. This rule of sampling is realized in determining the winning lottery tickets out of the total number of lottery tickets, considered to be the population which, on account of its nature, must necessarily be finite.
In mathematical statistics it is customary to refer to the results of any homogeneous observations as a "sample" , even if these results do not fit the concept of a population as explained above. For instance, the results of determination of some physical constant, subject to random errors, are often also referred to as a sample taken out of an infinite population. It is assumed that, in principle, it is possible to carry out any number of such measurements; the results actually obtained are considered as a sample of the infinite set of possible results, which is referred to as the population. In so doing it is assumed that the sampling rule is defined by a distribution function 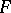 , so that the probability of obtaining an experimental result comprised in a semi-interval
, so that the probability of obtaining an experimental result comprised in a semi-interval 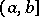 is expressed by the difference
is expressed by the difference 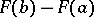 .
.
The concept of an infinite population is not logically unobjectionable and is not indispensable. In the solution of statistical problems one does not need the population itself, but rather some characteristics of the corresponding distribution function 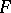 . From the point of view of probability theory, a sample drawn from an infinite population represents the observed values of certain random values with a given distribution law. In particular, if these variables are independent and identically distributed, their observed values are known as a simple sample. If this interpretation of the term "sample" is accepted, the introduction of the additional term "population" becomes superfluous.
. From the point of view of probability theory, a sample drawn from an infinite population represents the observed values of certain random values with a given distribution law. In particular, if these variables are independent and identically distributed, their observed values are known as a simple sample. If this interpretation of the term "sample" is accepted, the introduction of the additional term "population" becomes superfluous.
General aggregate. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=General_aggregate&oldid=13840