Gauss theorem
(teorema egregium)
The Gaussian curvature (the product of the principal curvatures) of a regular surface in Euclidean space  remains unchanged when the surface is isometrically deformed. ( "Regularity" here means
remains unchanged when the surface is isometrically deformed. ( "Regularity" here means  -smooth immersion.) Gauss' theorem follows from the fact that the Gaussian curvature
-smooth immersion.) Gauss' theorem follows from the fact that the Gaussian curvature  of a surface at a point
of a surface at a point  can be expressed in terms of the coefficients of the first fundamental form of the surface,
can be expressed in terms of the coefficients of the first fundamental form of the surface,
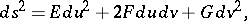 |
and their first and second derivatives at that point. Such an expression for  is called the Gauss equation, which may be written down in several forms [2]. The Gauss equation simplifies in special coordinates. Thus, in isothermal coordinates (
is called the Gauss equation, which may be written down in several forms [2]. The Gauss equation simplifies in special coordinates. Thus, in isothermal coordinates ( ,
,  ):
):
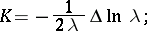 |
in semi-geodesic coordinates (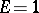 ,
, 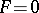 ):
):
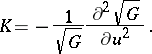 |
The Gauss equation and the Peterson–Codazzi equations form the conditions for the integrability of the system to which the problem of the reconstruction of a surface from its first and second fundamental forms may be reduced. It follows from Gauss' theorem and from the Gauss–Bonnet theorem that the difference between the sum of the angles of a geodesic triangle on a regular surface and 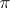 is equal to the oriented area of the spherical image of this triangle [1].
is equal to the oriented area of the spherical image of this triangle [1].
Gauss' theorem was established by C.F. Gauss [1] and it is the first and most important result in the study of the relations between the intrinsic and the extrinsic geometry of surfaces.
The following generalization of Gauss' theorem is valid [3], [4] for a regular 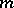 -dimensional, surface
-dimensional, surface 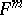 in a Riemannian space
in a Riemannian space 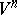 ,
,  :
:
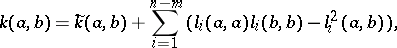 | (*) |
where  ,
,  are the sectional curvatures of, respectively,
are the sectional curvatures of, respectively, 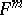 and
and 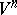 in the two-dimensional direction defined by the tangent vectors
in the two-dimensional direction defined by the tangent vectors  to
to 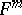 at the point under consideration, and
at the point under consideration, and  is the second fundamental form of
is the second fundamental form of 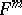 with respect to the
with respect to the  -th normal of an orthonormal set of normals at this point. It follows from (*) that, for a hypersurface
-th normal of an orthonormal set of normals at this point. It follows from (*) that, for a hypersurface 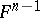 in
in 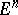 , all even elementary symmetric functions of the principal curvatures
, all even elementary symmetric functions of the principal curvatures
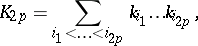 |
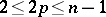 , are defined by the first fundamental form of
, are defined by the first fundamental form of 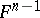 . In an even-dimensional space
. In an even-dimensional space 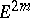 ,
, 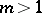 , a hypersurface
, a hypersurface 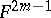 is uniquely defined by its first fundamental form and by the Gauss–Kronecker curvature
is uniquely defined by its first fundamental form and by the Gauss–Kronecker curvature
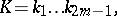 |
on the condition that the latter is non-zero [5].
For large classes of two-dimensional irregular surfaces in 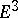 it is possible to define an "external curvatureexternal curvature" as a Borel measure connected with the spherical mapping and an "intrinsic curvatureintrinsic curvature" as a measure connected with the difference between the sum of the angles of a triangle and
it is possible to define an "external curvatureexternal curvature" as a Borel measure connected with the spherical mapping and an "intrinsic curvatureintrinsic curvature" as a measure connected with the difference between the sum of the angles of a triangle and  . A generalization of Gauss' theorem is the statement that the external and the internal curvatures coincide. Such a generalization of Gauss' theorem was obtained for general convex surfaces [6] and for
. A generalization of Gauss' theorem is the statement that the external and the internal curvatures coincide. Such a generalization of Gauss' theorem was obtained for general convex surfaces [6] and for 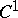 -smooth surfaces of bounded external curvature [7].
-smooth surfaces of bounded external curvature [7].
References
| [1] | C.F. Gauss, "Allgemeine Flächentheorie" , W. Engelmann , Leipzig (1900) (Translated from Latin) |
| [2] | W. Blaschke, "Einführung in die Differentialgeometrie" , Springer (1950) |
| [3] | D. Gromoll, W. Klingenberg, W. Meyer, "Riemannsche Geometrie im Grossen" , Springer (1968) |
| [4] | L.P. Eisenhart, "Riemannian geometry" , Princeton Univ. Press (1949) |
| [5] | S. Sternberg, "Lectures on differential geometry" , Prentice-Hall (1964) |
| [6] | A.D. Aleksandrov, "Die innere Geometrie der konvexen Flächen" , Akademie Verlag (1955) (Translated from Russian) |
| [7] | A.V. Pogorelov, "Extrinsic geometry of convex surfaces" , Amer. Math. Soc. (1972) (Translated from Russian) |
Comments
The Peterson–Codazzi equations are better known as the Mainardi–Codazzi equations.
References
| [a1] | M. Berger, B. Gostiaux, "Differential geometry: manifolds, curves, and surfaces" , Springer (1988) (Translated from French) |
| [a2] | P. Dombrowski, "150 years after Gauss" Astérisque , 62 (1979) |
| [a3] | M.P. Do Carmo, "Differential geometry of curves and surfaces" , Prentice-Hall (1976) pp. 145 |
| [a4] | S. Kobayashi, K. Nomizu, "Foundations of differential geometry" , 2 , Interscience (1969) |
| [a5] | M. Spivak, "A comprehensive introduction to differential geometry" , 1979 , Publish or Perish pp. 1–5 |
Gauss theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Gauss_theorem&oldid=15763