Gauss decomposition
of a topological group 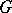
A representation of an everywhere-dense subset 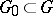 in the form
in the form 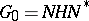 , where
, where 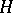 is an Abelian subgroup of
is an Abelian subgroup of 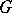 , and
, and 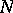 and
and 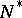 are nilpotent groups of
are nilpotent groups of 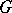 , normalized by
, normalized by 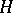 . If
. If 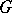 is the group
is the group 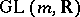 of non-singular real matrices of order
of non-singular real matrices of order 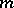 ,
, 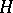 is the subgroup of diagonal matrices,
is the subgroup of diagonal matrices, 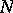 (respectively,
(respectively, 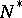 ) is the subgroup of lower-triangular (upper-triangular) matrices with unit elements on the principal diagonal, and
) is the subgroup of lower-triangular (upper-triangular) matrices with unit elements on the principal diagonal, and 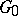 is the subset of matrices in
is the subset of matrices in  whose principal minors are non-zero, then the decomposition
whose principal minors are non-zero, then the decomposition 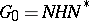 is known as the Gauss decomposition of the general linear group and is directly connected with the Gauss method for the solution of systems of linear equations: If
is known as the Gauss decomposition of the general linear group and is directly connected with the Gauss method for the solution of systems of linear equations: If 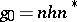 , where
, where 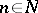 ,
, 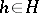 ,
, 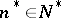 , is the non-singular coefficient matrix of the system of linear equations
, is the non-singular coefficient matrix of the system of linear equations 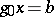 , then it may be converted by the Gauss method into the triangular form
, then it may be converted by the Gauss method into the triangular form 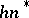 by multiplying it from the left by the lower-triangular matrix
by multiplying it from the left by the lower-triangular matrix 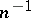 ,
, 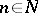 . A rigorous definition of the Gauss decomposition necessitates the introduction of the following terms. Let
. A rigorous definition of the Gauss decomposition necessitates the introduction of the following terms. Let 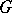 be a topological group, let
be a topological group, let  be a subgroup of it, and let
be a subgroup of it, and let 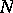 and
and 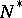 be nilpotent subgroups in
be nilpotent subgroups in 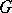 , normalized by
, normalized by 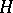 . The subgroup
. The subgroup 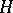 is called a triangular truncation of
is called a triangular truncation of 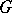 if: 1)
if: 1) 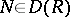 ,
, 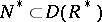 , where
, where 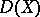 is the commutator subgroup of the group
is the commutator subgroup of the group 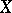 and
and 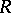 and
and 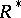 are connected solvable subgroups of
are connected solvable subgroups of 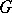 ; and 2) the set
; and 2) the set 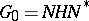 is everywhere dense in
is everywhere dense in 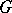 , and the decomposition
, and the decomposition 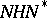 is unique. The decomposition
is unique. The decomposition 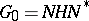 is called a triangular decomposition in
is called a triangular decomposition in 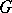 . If
. If 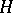 is an Abelian group, this decomposition is called a completely-triangular decomposition or a Gauss decomposition. In such a case the subgroups
is an Abelian group, this decomposition is called a completely-triangular decomposition or a Gauss decomposition. In such a case the subgroups 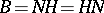 ,
, 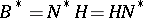 are solvable. Let
are solvable. Let 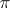 be an irreducible (continuous) representation of
be an irreducible (continuous) representation of 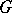 in a finite-dimensional vector space
in a finite-dimensional vector space 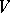 , and let
, and let 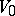 be the subspace of all vectors in
be the subspace of all vectors in 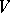 which are fixed with respect to
which are fixed with respect to 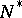 ;
;  will then be invariant with respect to
will then be invariant with respect to 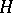 , while the representation
, while the representation 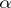 of
of 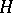 on
on 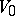 will be irreducible. The representation
will be irreducible. The representation 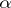 unambiguously defines
unambiguously defines 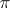 , up to an equivalence. Let
, up to an equivalence. Let 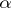 also denote the representation of
also denote the representation of 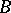 on
on 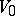 restricting to
restricting to 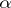 on
on 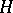 and being trivial on
and being trivial on 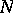 . Let
. Let 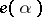 denote the representation of
denote the representation of 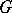 on the vector space
on the vector space 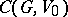 induced by this
induced by this 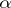 . Then
. Then 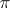 is contained (as an invariant part) in
is contained (as an invariant part) in 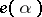 , and the space
, and the space  is one-dimensional. If
is one-dimensional. If 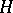 is an Abelian subgroup, then
is an Abelian subgroup, then 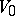 is one-dimensional and
is one-dimensional and  is a character of the group
is a character of the group 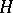 . The following examples of triangular decompositions of Lie groups are known. 1) Let
. The following examples of triangular decompositions of Lie groups are known. 1) Let 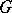 be a reductive connected complex Lie group with Cartan subalgebra
be a reductive connected complex Lie group with Cartan subalgebra 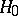 and let
and let 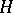 be a reductive connected subgroup in
be a reductive connected subgroup in 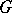 containing
containing 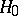 . The subgroup
. The subgroup 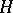 is then a triangular truncation of
is then a triangular truncation of 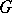 . 2) Let
. 2) Let 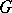 be a reductive connected linear Lie group;
be a reductive connected linear Lie group; 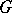 will then contain a triangular truncation
will then contain a triangular truncation 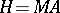 , where
, where 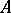 is a simply-connected Abelian subgroup in
is a simply-connected Abelian subgroup in 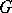 (generated by the non-compact roots in the Lie algebra of
(generated by the non-compact roots in the Lie algebra of 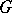 ), and
), and 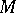 is the centralizer of
is the centralizer of  in the maximal compact subgroup
in the maximal compact subgroup 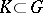 . 3) In particular, any reductive connected complex Lie group permits a Gauss decomposition
. 3) In particular, any reductive connected complex Lie group permits a Gauss decomposition 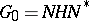 , where
, where 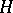 is the Cartan subgroup of
is the Cartan subgroup of 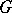 and
and 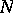 (respectively
(respectively 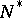 ) is an analytic subgroup in
) is an analytic subgroup in 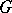 whose Lie algebra is spanned by all root vectors
whose Lie algebra is spanned by all root vectors 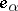 ,
, 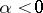 (respectively
(respectively 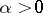 ), with
), with 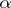 denoting the roots with respect to
denoting the roots with respect to 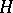 , i.e.
, i.e. 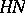 and
and 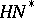 are opposite Borel subgroups (cf. Borel subgroup). In examples 1)–3) the subgroups
are opposite Borel subgroups (cf. Borel subgroup). In examples 1)–3) the subgroups 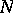 and
and 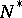 are simply connected,
are simply connected, 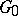 is open in
is open in 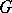 in the Zariski topology, while the mapping
in the Zariski topology, while the mapping 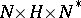 ,
, 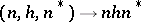 , is an isomorphism of algebraic varieties (and, in particular, a homeomorphism). This implies that the algebraic variety
, is an isomorphism of algebraic varieties (and, in particular, a homeomorphism). This implies that the algebraic variety 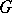 is rational.
is rational.
References
| [1] | D.P. Zhelobenko, "Compact Lie groups and their representations" , Amer. Math. Soc. (1973) (Translated from Russian) |
Gauss decomposition. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Gauss_decomposition&oldid=18870