Galois ring
The Galois ring 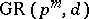 is [a5] the unique Galois extension of
is [a5] the unique Galois extension of  of degree
of degree 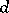 . For instance
. For instance 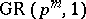 is
is  and
and  is
is  . Generalizing finite fields (cf. Finite field), these rings find applications in similar areas: linear recurrences [a1], [a6], [a7], cyclic codes [a9], [a2] [a3], association schemes [a10], and character sums [a10], [a4]. For a connection with Witt rings see [a8] (cf. also Witt ring). Two different constructions of these rings are given below: bottom-up, starting from a finite field, and top-down, starting from a local field.
. Generalizing finite fields (cf. Finite field), these rings find applications in similar areas: linear recurrences [a1], [a6], [a7], cyclic codes [a9], [a2] [a3], association schemes [a10], and character sums [a10], [a4]. For a connection with Witt rings see [a8] (cf. also Witt ring). Two different constructions of these rings are given below: bottom-up, starting from a finite field, and top-down, starting from a local field.
Bottom up.
This is the first and the most algorithmic one. Let  . Pick an irreducible monic primitive polynomial
. Pick an irreducible monic primitive polynomial  of degree
of degree 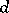 , as in the standard construction of
, as in the standard construction of  from
from  , and lift it to a polynomial
, and lift it to a polynomial  over
over  in such a way that the nice finite field property (
in such a way that the nice finite field property ( divides
divides  ) still holds. In the language of linear recurrences (or linear feedback shift registers), one has lifted an
) still holds. In the language of linear recurrences (or linear feedback shift registers), one has lifted an 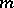 -sequence of period
-sequence of period  over
over 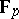 into a linear recurrence over
into a linear recurrence over  of the same period. This is construction
of the same period. This is construction  of [a1]. Note that an arbitrary lift will lead to multiplying the period by a power of
of [a1]. Note that an arbitrary lift will lead to multiplying the period by a power of 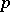 , as in construction
, as in construction 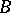 of [a1]. For example,
of [a1]. For example,  ,
,  gives a period
gives a period 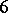 and not
and not  . Now, let
. Now, let
 |
Top down.
This 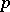 -adic approach was introduced in print in [a4] but was implicitly known to M. Yamada [a10], who used the term "Teichmüller" , as in
-adic approach was introduced in print in [a4] but was implicitly known to M. Yamada [a10], who used the term "Teichmüller" , as in 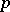 -adic analysis, and also to E. Spiegel [a9]. Denote by
-adic analysis, and also to E. Spiegel [a9]. Denote by  the ring of
the ring of 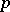 -adic integers, best viewed as the set of formal expansions in powers of
-adic integers, best viewed as the set of formal expansions in powers of  with coefficients in the residue field
with coefficients in the residue field  . Then
. Then 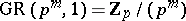 . For higher values of
. For higher values of 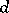 one considers the unramified extension of
one considers the unramified extension of  generated by
generated by  (an
(an  -th root of unity) and its ring of integers
-th root of unity) and its ring of integers  . Let
. Let 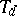 denote the set of
denote the set of  roots of
roots of 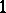 over this latter ring. This set of so-called Teichmüller representatives reduces modulo
over this latter ring. This set of so-called Teichmüller representatives reduces modulo 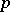 to
to 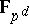 . The ring of integers of the
. The ring of integers of the 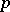 -adic field admits the following expansion:
-adic field admits the following expansion:  , which converges in the sense of the
, which converges in the sense of the 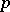 -adic valuation. Modulo
-adic valuation. Modulo  this yields
this yields
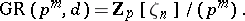 |
Multiplicative structure.
The ring  comprises units
comprises units  and zero divisors
and zero divisors  . The multiplicative group
. The multiplicative group 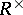 is the direct product of
is the direct product of  by the group of so-called principal units
by the group of so-called principal units  . The group of principal units is isomorphic, for
. The group of principal units is isomorphic, for  or
or  , to the additive group of
, to the additive group of 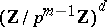 . The Galois group of
. The Galois group of 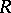 over
over  is isomorphic to the Galois group of
is isomorphic to the Galois group of  over
over 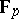 and therefore cyclic of order
and therefore cyclic of order 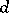 .
.
References
| [a1] | S. Boztas, A.R. Hammons, P.V. Kumar, "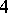 -phase sequence with near optimum correlation properties" IEEE Inform. Th. , 38 (1992) pp. 1101–1113 -phase sequence with near optimum correlation properties" IEEE Inform. Th. , 38 (1992) pp. 1101–1113 |
| [a2] | A. Bonnecaze, P. Solé, A.R. Calderbank, "Quaternary construction of unimodular lattices" IEEE Inform. Th. , 41 (1995) pp. 366–376 |
| [a3] | A.R. Hammons, P.V. Kumar, A.R. Calderbank, N.J.A. Sloane, P. Solé, "The 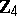 -linearity of Kerdock, Preparata, Goethals, and related codes" IEEE Trans. Information Th. , 40 (1994) pp. 301–319 -linearity of Kerdock, Preparata, Goethals, and related codes" IEEE Trans. Information Th. , 40 (1994) pp. 301–319 |
| [a4] | V. Kumar, T. Helleseth, R.A. Calderbank, "An upper bound for Weil-type exponential sums over Galois rings and applications" IEEE Inform. Th. , 41 (1995) |
| [a5] | B.R. MacDonald, "Finite rings with identity" , M. Dekker (1974) |
| [a6] | P. Solé, "A quaternary cyclic code and a family of quaternary sequences with low correlation" G. Cohen (ed.) J. Wolfmann (ed.) , Coding Theory and Applications , Lecture Notes in Computer Science , 388 , Springer (1989) pp. 193–201 |
| [a7] | P. Udaya, M.U. Siddiqui, "Optimal biphase sequences with large linear complexity derived from sequences over 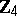 " IEEE Inform. Th. , IT–42 (1996) pp. 202–216 " IEEE Inform. Th. , IT–42 (1996) pp. 202–216 |
| [a8] | A.G. Shanbag, P.V. Kumar, T. Helleseth, "An upperbound for the extended Kloosterman sums over Galois rings" , Finite Fields and Applications (to appear) |
| [a9] | E. Spiegel, "Codes over 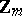 revisited" Inform. and Control , 37 (1978) pp. 100–104 revisited" Inform. and Control , 37 (1978) pp. 100–104 |
| [a10] | M. Yamada, "Distance regular graphs of girth 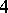 over an extension ring of over an extension ring of 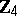 " Graphs and Combinatorics , 6 (1980) pp. 381–384 " Graphs and Combinatorics , 6 (1980) pp. 381–384 |
Galois ring. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Galois_ring&oldid=14749