Galois correspondence
From Encyclopedia of Mathematics
between two partially ordered sets  and
and 
A pair of mappings  and
and  which satisfy the following conditions:
which satisfy the following conditions:
if  , then
, then  ;
;
if  , then
, then  ;
;
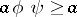 and
and 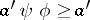 .
.
Here 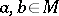 ,
, 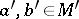 .
.
The concept of a Galois correspondence is closely connected with the concept of closure in a partially ordered set; this means that if a Galois correspondence is established between 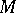 and
and  , the equalities
, the equalities  ,
, 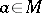 , and
, and 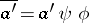 ,
, 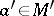 , define closure operations (cf. Closure relation) in
, define closure operations (cf. Closure relation) in 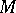 and
and 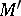 , respectively. The concept of a Galois correspondence originated in Galois theory, which deals with the Galois correspondence between all intermediate subfields of an extension
, respectively. The concept of a Galois correspondence originated in Galois theory, which deals with the Galois correspondence between all intermediate subfields of an extension 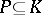 and the system of subgroups of the Galois group of this extension.
and the system of subgroups of the Galois group of this extension.
References
| [1] | P.M. Cohn, "Universal algebra" , Reidel (1981) |
| [2] | A.G. Kurosh, "Lectures on general algebra" , Chelsea (1963) (Translated from Russian) |
How to Cite This Entry:
Galois correspondence. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Galois_correspondence&oldid=12061
Galois correspondence. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Galois_correspondence&oldid=12061
This article was adapted from an original article by O.A. Ivanova (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article