G-structure
on a manifold
A principal subbundle with structure group  of the principal bundle of co-frames on the manifold. More exactly, let
of the principal bundle of co-frames on the manifold. More exactly, let  be the principal
be the principal  -bundle of all co-frames of order
-bundle of all co-frames of order 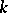 over an
over an  -dimensional manifold
-dimensional manifold 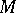 , and let
, and let 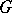 be a subgroup of the general linear group
be a subgroup of the general linear group 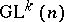 of order
of order 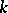 . A submanifold
. A submanifold 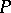 of the manifold of
of the manifold of 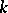 -co-frames
-co-frames 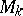 defines a
defines a 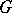 -structure of order
-structure of order  ,
, 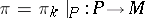 , if
, if 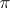 defines a principal
defines a principal 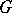 -bundle, i.e. the fibres of
-bundle, i.e. the fibres of 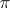 are orbits of
are orbits of 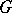 . For example, a section
. For example, a section 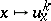 of
of 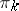 (a field of co-frames) defines a
(a field of co-frames) defines a 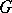 -structure
-structure 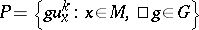 , which is called the
, which is called the  -structure generated by this field of co-frames. Any
-structure generated by this field of co-frames. Any 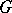 -structure is locally generated by a field of co-frames. The
-structure is locally generated by a field of co-frames. The  -structure over the space
-structure over the space 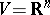 generated by the field of co-frames
generated by the field of co-frames 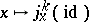 , where
, where 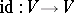 is the identity mapping, is called the standard flat
is the identity mapping, is called the standard flat 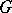 -structure.
-structure.
Let  be a
be a 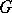 -structure. The mapping of the manifold
-structure. The mapping of the manifold 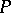 into the point
into the point 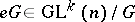 can be extended to a
can be extended to a 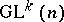 -equivariant mapping
-equivariant mapping 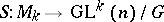 , which can be considered as a structure of type
, which can be considered as a structure of type 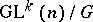 on
on 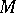 . If the homogeneous space
. If the homogeneous space 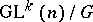 is imbedded as an orbit in a vector space
is imbedded as an orbit in a vector space  admitting a linear action of
admitting a linear action of 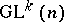 , then the structure
, then the structure 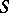 can be considered as a linear structure of type
can be considered as a linear structure of type 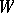 ; this is called the Bernard tensor of the
; this is called the Bernard tensor of the  -structure
-structure 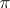 , and is often identified with it. Conversely, let
, and is often identified with it. Conversely, let 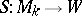 be a linear geometric structure of type
be a linear geometric structure of type 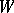 (for example, a tensor field), whereby
(for example, a tensor field), whereby 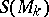 belongs to a single orbit
belongs to a single orbit 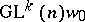 of
of  .
. 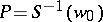 is then a
is then a 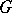 -structure, where
-structure, where 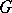 is the stabilizer of the point
is the stabilizer of the point 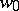 in
in 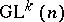 , and
, and 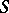 is its Bernard tensor. For example, a Riemannian metric defines an
is its Bernard tensor. For example, a Riemannian metric defines an 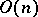 -structure, an almost-symplectic structure defines a
-structure, an almost-symplectic structure defines a 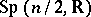 -structure, an almost-complex structure defines a
-structure, an almost-complex structure defines a 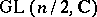 -structure, and a torsion-free connection defines a
-structure, and a torsion-free connection defines a 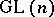 -structure of the second order (
-structure of the second order (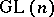 is considered here as a subgroup of the group
is considered here as a subgroup of the group 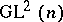 ). An affinor (a field of endomorphisms) defines a
). An affinor (a field of endomorphisms) defines a 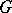 -structure if and only if it has at all points one and the same Jordan normal form
-structure if and only if it has at all points one and the same Jordan normal form 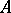 , where
, where 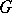 is the centralizer of the matrix
is the centralizer of the matrix 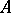 in
in 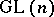 .
.
The elements of the manifold  can be considered as co-frames of order 1 on
can be considered as co-frames of order 1 on  , which makes it possible to consider the natural bundle
, which makes it possible to consider the natural bundle 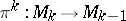 as an
as an  -structure of order one, where
-structure of order one, where 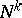 is the kernel of the natural homomorphism
is the kernel of the natural homomorphism 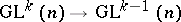 . Every
. Every 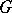 -structure
-structure 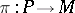 of order
of order 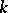 has a related sequence of
has a related sequence of 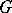 -structures of order one,
-structures of order one,
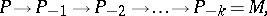 |
where 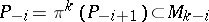 . Consequently, the study of
. Consequently, the study of 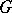 -structures of higher order reduces to the study of
-structures of higher order reduces to the study of  -structures of order one. A co-frame
-structures of order one. A co-frame 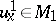 can be considered as an isomorphism
can be considered as an isomorphism 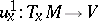 .
.
The 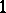 -form
-form 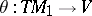 , assigning to a vector
, assigning to a vector 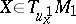 the value
the value 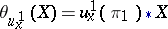 , is called the displacement form. In the local coordinates
, is called the displacement form. In the local coordinates 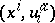 of
of 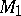 , the form
, the form 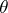 is expressed as
is expressed as 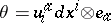 , where
, where 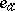 is the standard basis in
is the standard basis in 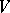 .
.
The restriction  of
of 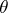 on a
on a  -structure
-structure 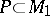 is called the displacement form of the
is called the displacement form of the 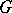 -structure. It possesses the following properties: 1) strong horizontality:
-structure. It possesses the following properties: 1) strong horizontality: 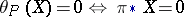 ; and 2)
; and 2) 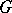 -equivariance:
-equivariance: 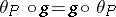 for any
for any 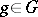 .
.
Using the form  it is possible to characterize the principal bundles with base
it is possible to characterize the principal bundles with base 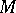 that are isomorphic to a
that are isomorphic to a 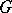 -structure. Namely, a principal
-structure. Namely, a principal 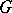 -bundle
-bundle 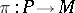 is isomorphic to a
is isomorphic to a 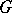 -structure if and only if there are a faithful linear representation
-structure if and only if there are a faithful linear representation 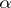 of the group
of the group 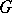 in an
in an  -dimensional vector space
-dimensional vector space 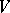 ,
,  , and a
, and a 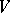 -valued strongly-horizontal
-valued strongly-horizontal  -equivariant
-equivariant 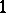 -form
-form 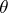 on
on 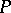 . Removal of the requirement that the representation
. Removal of the requirement that the representation 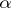 be faithful gives the concept of a generalized
be faithful gives the concept of a generalized 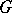 -structure (of order one) on
-structure (of order one) on 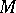 , namely a principal
, namely a principal 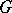 -bundle
-bundle 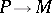 with a linear representation
with a linear representation 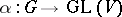 ,
,  , and a
, and a 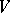 -valued strongly-horizontal
-valued strongly-horizontal 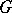 -equivariant
-equivariant 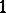 -form
-form 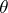 on
on 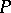 .
.
An example of a generalized 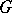 -structure is the canonical bundle
-structure is the canonical bundle 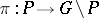 over the homogeneous space
over the homogeneous space 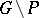 of a Lie group
of a Lie group 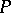 . Here
. Here 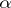 is the isotropy representation of the group
is the isotropy representation of the group 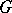 , while
, while 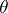 is defined by the Maurer–Cartan form of
is defined by the Maurer–Cartan form of 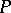 .
.
Let 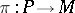 be a
be a 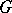 -structure of order one. The bundle
-structure of order one. The bundle 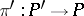 of
of 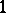 -jets of local sections of
-jets of local sections of 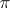 can be considered as a
can be considered as a 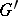 -structure on
-structure on 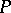 , where
, where  is a commutative group,
is a commutative group, 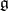 is the Lie algebra of
is the Lie algebra of 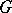 , that is linearly represented in the space
, that is linearly represented in the space 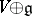 by the formula
by the formula
 |
and that acts on the manifold 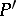 according to the formula
according to the formula
 |
where 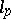 is the canonical isomorphism of the Lie algebra
is the canonical isomorphism of the Lie algebra 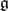 of the group
of the group 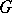 onto the vertical subspace
onto the vertical subspace  . Here the element
. Here the element 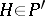 is considered as a horizontal (i.e. complementary to the vertical) subspace in
is considered as a horizontal (i.e. complementary to the vertical) subspace in 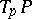 . It defines a co-frame
. It defines a co-frame 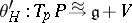 , which is defined on a vertical subspace by the mapping
, which is defined on a vertical subspace by the mapping 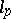 , and on a horizontal subspace by the mapping
, and on a horizontal subspace by the mapping  . The vector function
. The vector function 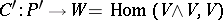 , defined by the formula
, defined by the formula 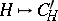 ,
, 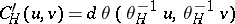 , is called the torsion function of the
, is called the torsion function of the  -structure
-structure  . A section
. A section 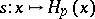 of the bundle
of the bundle 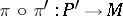 defines a connection on
defines a connection on 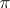 , while the restriction of the function
, while the restriction of the function 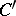 on
on 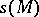 is a function defining the coordinates of the torsion tensor of this connection relative to the field of co-frames
is a function defining the coordinates of the torsion tensor of this connection relative to the field of co-frames  .
.
The mapping 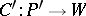 is
is 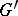 -equivariant relative to the above-mentioned action of
-equivariant relative to the above-mentioned action of 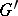 on
on 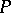 and to the action of
and to the action of 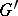 on
on 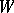 , which is defined by the formula
, which is defined by the formula
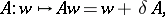 |
where 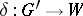 ,
, 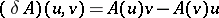 . The mapping
. The mapping 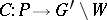 induced by the mapping
induced by the mapping 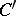 is called the structure function of the
is called the structure function of the 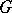 -structure
-structure 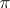 , the vanishing of
, the vanishing of 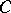 is equivalent to the existence of a torsion-free connection on
is equivalent to the existence of a torsion-free connection on  .
.
The choice of a subspace 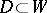 complementary to
complementary to 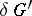 defines a subbundle
defines a subbundle 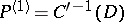 of the bundle of co-frames
of the bundle of co-frames 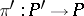 with structure group
with structure group 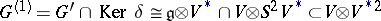 , i.e. a
, i.e. a  -structure
-structure 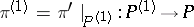 on
on 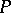 . It is called the first prolongation of the
. It is called the first prolongation of the 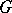 -structure
-structure 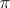 . The
. The  -th prolongation
-th prolongation  is defined by induction as the
is defined by induction as the 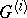 -structure on
-structure on 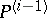 , where the group
, where the group 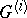 is isomorphic to the vector group
is isomorphic to the vector group 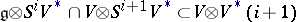 . The structure function
. The structure function 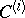 of the
of the 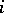 -th prolongation is called the structure function of
-th prolongation is called the structure function of  -th order of the
-th order of the 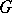 -structure
-structure 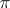 .
.
The central problem of the theory of 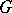 -structures is the local equivalence problem, i.e. the problem of finding necessary and sufficient conditions under which two
-structures is the local equivalence problem, i.e. the problem of finding necessary and sufficient conditions under which two  -structures
-structures 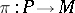 and
and 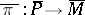 with the same structure group
with the same structure group 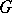 are locally equivalent, i.e. a local diffeomorphism
are locally equivalent, i.e. a local diffeomorphism  of the manifolds
of the manifolds 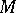 and
and 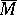 should exist that induces an isomorphism of
should exist that induces an isomorphism of 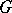 -structures over the neighbourhoods
-structures over the neighbourhoods 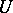 and
and 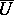 . A particular case of this problem is the integrability problem, i.e. the problem of finding necessary and sufficient conditions for the local equivalence of a given
. A particular case of this problem is the integrability problem, i.e. the problem of finding necessary and sufficient conditions for the local equivalence of a given 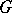 -structure and the standard flat
-structure and the standard flat 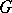 -structure. The local equivalence problem can be reformulated as the problem of finding a complete system of local invariants of a
-structure. The local equivalence problem can be reformulated as the problem of finding a complete system of local invariants of a 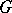 -structure.
-structure.
For an 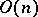 -structure, which is identified with a Riemannian metric, the integrability problem was solved by B. Riemann: Necessary and sufficient conditions for integrability consist in the vanishing of the curvature tensor of the metric. The local equivalence problem was solved by E. Christoffel and R. Lipschitz: A complete system of local invariants of a Riemannian metric consists of its curvature tensor and its successive covariant derivatives (see [1]).
-structure, which is identified with a Riemannian metric, the integrability problem was solved by B. Riemann: Necessary and sufficient conditions for integrability consist in the vanishing of the curvature tensor of the metric. The local equivalence problem was solved by E. Christoffel and R. Lipschitz: A complete system of local invariants of a Riemannian metric consists of its curvature tensor and its successive covariant derivatives (see [1]).
An approach to solving the equivalence problem is based on the concepts of a prolongation and a structure function. Every 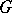 -structure
-structure 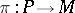 of order one with structure group
of order one with structure group 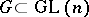 is connected with a sequence of prolongations
is connected with a sequence of prolongations
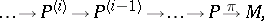 |
and a sequence of structure functions 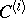 . For an
. For an 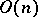 -structure, the structure function
-structure, the structure function 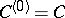 on
on 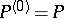 is equal to 0, while the essential parts of the remaining structure functions
is equal to 0, while the essential parts of the remaining structure functions 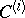 ,
, 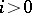 , are identified with the curvature tensor of the corresponding metric and its successive covariant derivatives. For
, are identified with the curvature tensor of the corresponding metric and its successive covariant derivatives. For 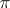 to be integrable it is necessary and sufficient that the structure functions
to be integrable it is necessary and sufficient that the structure functions 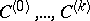 be constant, and that their values coincide with the corresponding values of the structure functions of the standard flat
be constant, and that their values coincide with the corresponding values of the structure functions of the standard flat 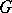 -structure (see [6], [8], [9]). The number
-structure (see [6], [8], [9]). The number  depends only on the group
depends only on the group 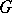 . For a broad class of linear groups, especially for all irreducible groups
. For a broad class of linear groups, especially for all irreducible groups 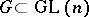 that do not belong to Berger's list of holonomy groups of spaces with a torsion-free affine connection [3], one has
that do not belong to Berger's list of holonomy groups of spaces with a torsion-free affine connection [3], one has 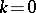 , and for a
, and for a 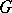 -structure to be integrable it is necessary and sufficient that the structure function
-structure to be integrable it is necessary and sufficient that the structure function 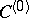 vanishes, or that a torsion-free linear connection exists, preserving the
vanishes, or that a torsion-free linear connection exists, preserving the 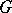 -structure.
-structure.
A 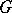 -structure
-structure 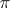 is called a
is called a 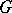 -structure of finite type (equal to
-structure of finite type (equal to 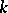 ) if
) if 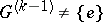 ,
, 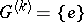 . In this case
. In this case 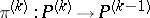 is a field of co-frames (an absolute parallelism), and the automorphism group of the
is a field of co-frames (an absolute parallelism), and the automorphism group of the 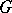 -structure
-structure 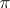 is isomorphic to the automorphism group of this parallelism and is a Lie group. The local equivalence problem of these structures reduces to the equivalence problem of absolute parallelisms and has been solved in terms of a finite sequence of structure functions (see [2]). For a
is isomorphic to the automorphism group of this parallelism and is a Lie group. The local equivalence problem of these structures reduces to the equivalence problem of absolute parallelisms and has been solved in terms of a finite sequence of structure functions (see [2]). For a 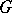 -structure of infinite type, the local equivalence problem remains unsolved in the general case (1984).
-structure of infinite type, the local equivalence problem remains unsolved in the general case (1984).
Two 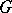 -structures
-structures 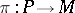 and
and 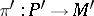 are called formally equivalent at the points
are called formally equivalent at the points 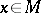 ,
, 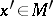 if an isomorphism of the fibres
if an isomorphism of the fibres 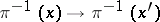 exists that can be continued to an isomorphism of the corresponding fibres of the prolongations
exists that can be continued to an isomorphism of the corresponding fibres of the prolongations 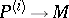 and
and 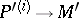
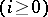 . Examples have been found which demonstrate that if two
. Examples have been found which demonstrate that if two 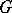 -structures of class
-structures of class 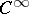 are formally equivalent for all pairs
are formally equivalent for all pairs 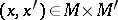 , then it does not follow, generally speaking, that they are locally equivalent [6]. In the analytic case, proper subsets
, then it does not follow, generally speaking, that they are locally equivalent [6]. In the analytic case, proper subsets 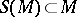 ,
, 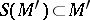 exist, which are countable unions of analytic sets, such that for any
exist, which are countable unions of analytic sets, such that for any 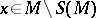 ,
, 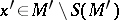 , the formal equivalence of two structures
, the formal equivalence of two structures 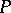 and
and 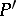 at the points
at the points 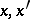 implies that they are locally equivalent [7].
implies that they are locally equivalent [7].
References
| [1] | S. Kobayashi, K. Nomizu, "Foundations of differential geometry" , 1 , Wiley (1963) |
| [2] | S. Sternberg, "Lectures on differential geometry" , Prentice-Hall (1964) |
| [3] | M. Berger, "Sur les groupes d'holonomie homogène des variétés à connexion affine et des variétés riemanniennes" Bull. Soc. Math. France , 83 (1955) pp. 279–330 |
| [4] | S.S. Chern, "The geometry of 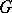 -structures" Bull. Amer. Math. Soc. , 72 (1966) pp. 167–219 -structures" Bull. Amer. Math. Soc. , 72 (1966) pp. 167–219 |
| [5] | S. Kobayashi, "Transformation groups in differential geometry" , Springer (1972) |
| [6] | P. Molino, "Théorie des 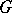 -structures: le problème d'Aeequivalence" , Springer (1977) -structures: le problème d'Aeequivalence" , Springer (1977) |
| [7] | T. Morimoto, "Sur le problème d'équivalence des structures géométriques" C.R. Acad. Sci. Paris , 292 : 1 (1981) pp. 63–66 (English summary) |
| [8] | I.M. Singer, S. Sternberg, "The infinite groups of Lie and Cartan. I. The transitive groups" J. d'Anal. Math. , 15 (1965) pp. 1–114 |
| [9] | A.S. Pollack, "The integrability problem for pseudogroup structures" J. Diff. Geom. , 9 : 3 (1974) pp. 355–390 |
G-structure. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=G-structure&oldid=16162