Functional-differential equation
Many real systems exhibit the phenomenon of after-effect, which means that future states of the system can depend not only on the present, but also on the past history. After-effect occurs in physics, chemistry, biology, economy, medicine, cybernetics, etc. This wide appearance of after-effect is a reason to consider it as a universal property of the surrounding world. An appropriate mathematical tool to investigate phenomena with after-effect is provided by the theory of functional-differential equations. Historically, the first functional-differential equations were considered by L. Euler, J. Bernoulli, J. Lagrange, P. Laplace, S.D. Poisson and others in the 18th century in connection with geometrical problems. In the 19th century, functional-differential equations were investigated rather occasionally. At the beginning of the 20th century, important applications of functional-differential equations in the mechanics of visco-elasticity and in ecology were found by V. Volterra [a5], [a6]. The situation changed radically in the 1930s due to a number of technical and scientific reasons. The basic elements of the modern theory of functional-differential equations were established in [a3], [a4]. The years after [a3] have witnessed an explosive development of the theory of functional-differential equations and their applications (see, e.g. [a1], [a7], [a8], [a9], [a10], [a11], [a12], [a13], [a14], [a2] and the numerous references therein).
A functional-differential equation (also called a differential equation with deviating argument, cf. also Differential equations, ordinary, with distributed arguments) can be considered as a combination of differential and functional equations. The values of the argument in a functional-differential equation can be discrete, continuous or mixed. Correspondingly, one introduce the notions of a differential-difference equation, an integro-differential equation, etc.
A functional-differential equation is called periodic with period 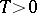 (briefly,
(briefly, 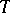 -periodic) if it is invariant under the change
-periodic) if it is invariant under the change 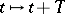 . This means that if one replaces
. This means that if one replaces 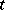 by
by 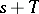 , sets
, sets 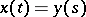 , and then replaces the letters
, and then replaces the letters 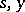 by
by 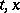 , then one should obtain the initial equation. A functional-differential equation is called autonomous if it is invariant under the change
, then one should obtain the initial equation. A functional-differential equation is called autonomous if it is invariant under the change 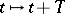 for all
for all 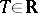 .
.
The order of a functional-differential equation is the order of the highest derivative of the unknown function entering in the equation. So, a functional equation may be regarded as a functional-differential equation of order zero. Hence, the notion of a functional-differential equation generalizes all equations of mathematical analysis for functions of a continuous argument. A similar assertion holds for functions depending on several arguments.
One can naturally define the notions of a functional-differential inequality or inclusion and of a stochastic functional-differential equation, which are similar to the definition of a functional-differential equation.
Consider the following functional-differential equation with finitely many argument deviations:
 | (a1) |
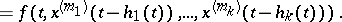 |
Here,  , and all
, and all 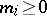 ,
, 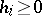 , i.e. all argument deviations are assumed to be non-negative. This property constitutes the definition of a functional-differential equation with retardations. In (a1), the function
, i.e. all argument deviations are assumed to be non-negative. This property constitutes the definition of a functional-differential equation with retardations. In (a1), the function 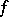 and the delays
and the delays 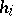 are given, and
are given, and  is the unknown function of
is the unknown function of 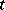 .
.
Equation (a1) is called:
a functional-differential equation of retarded type, or a retarded functional-differential equation (abbreviated RDE), if 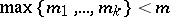 ;
;
a functional-differential equation of neutral type (abbreviated NDE) if  ;
;
a functional-differential equation of advanced type (abbreviated ADE) if 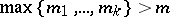 . In particular, a retarded functional-differential equation can be characterized as an equation in which the value of the higher derivative for any values of the arguments is defined by the values of the lower derivatives depending on the lesser values of the argument.
. In particular, a retarded functional-differential equation can be characterized as an equation in which the value of the higher derivative for any values of the arguments is defined by the values of the lower derivatives depending on the lesser values of the argument.
Sometimes functional-differential equations with discrete retardations are called equations with time lag, and equations with continuous retardations are called equations with after-effect.
Experience in mathematical modeling has shown that the evolution equations of actual processes with retardations are almost exclusively retarded or neutral functional-differential equations. On the other hand, the investigation of various problems for these equations has revealed that retarded or neutral functional-differential equations have many "nice" mathematical properties (in contrast to functional-differential equations of advanced type).
Equation (a1) can be transformed to a first-order vector equation of higher dimension by taking as new unknown functions the lower derivatives of  . Preserving the notation
. Preserving the notation  for the new unknown function and
for the new unknown function and  for the new right-hand side, one can write an RDE as
for the new right-hand side, one can write an RDE as
 | (a2) |
and an NDE as
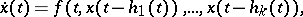 | (a3) |
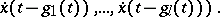 |
Note that any functional-differential equation is equivalent to a hybrid system of ordinary differential equations and functional equations, in particular, difference equations. For example, (a3) is equivalent to the following hybrid system:
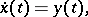 |
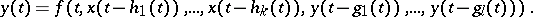 |
More complicated types of retardation have also be considered, and also have real applications. For example, the delay may depend on the unknown solution, and have the form 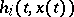 . Such delays are sometimes termed auto-regulative.
. Such delays are sometimes termed auto-regulative.
Similarly, functional-differential equations with retardation and continuous and mixed argument deviations may have the form of an integro-differential or functional integro-differential equation of some structure of Volterra type. The latter means that for any 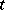 the integrals depend on the values of the unknown function
the integrals depend on the values of the unknown function  on some interval
on some interval 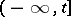 . For example, the continuous analogue of (a2) is the Volterra-type integro-differential equation
. For example, the continuous analogue of (a2) is the Volterra-type integro-differential equation
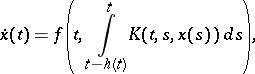 | (a4) |
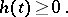 |
Certain classes of equations of the type (a4) can be naturally extended to other functional-differential equations. For example, if 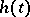 takes finite values only, then (a4) has finite after-effect; if
takes finite values only, then (a4) has finite after-effect; if 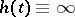 , it has infinite after-effect. If
, it has infinite after-effect. If 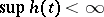 , then it has bounded after-effect, and it has unbounded after-effect in the opposite case. Sometimes the after-effect time is interpreted as
, then it has bounded after-effect, and it has unbounded after-effect in the opposite case. Sometimes the after-effect time is interpreted as 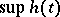 ; then finiteness, and infiniteness, of after-effect means boundedness, respectively unboundedness, of it.
; then finiteness, and infiniteness, of after-effect means boundedness, respectively unboundedness, of it.
If 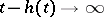 as
as 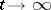 , then (a4) is said to have the property of completely forgetting the past. This means that the values of the solution
, then (a4) is said to have the property of completely forgetting the past. This means that the values of the solution  on any finite
on any finite 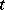 -interval do not influence the right-hand side of the equation for sufficiently large
-interval do not influence the right-hand side of the equation for sufficiently large 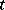 . In other words, the rate of change of the state at any moment is determined by the states of the process at preceding moments which are not too remote. Sometimes such equations are said to have fading memory. If
. In other words, the rate of change of the state at any moment is determined by the states of the process at preceding moments which are not too remote. Sometimes such equations are said to have fading memory. If 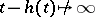 as
as 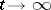 , then either the past is not forgotten (residual phenomena), or is asymptotically forgotten.
, then either the past is not forgotten (residual phenomena), or is asymptotically forgotten.
Sometimes, Volterra-type integro-differential equations can be reduced to an (in some sense) equivalent system of ordinary differential equations. Delays and equations with after-effect may have a more complicated structure, but they all have the Volterra property: the rate of evolution of the process depends on the past and the present, but not on the future. Keeping this property in mind, one can write the general retarded functional -differential equation in the form
 | (a5) |
Here, 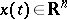 and
and 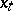 (for a given
(for a given 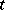 ) is the function defined by
) is the function defined by
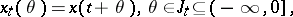 |
where 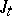 is a given interval
is a given interval 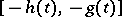 or
or 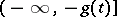 . Note that
. Note that 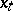 may be treated as the fragment of the function
may be treated as the fragment of the function  at the left to the point
at the left to the point 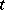 , observed from this point. The right-hand side of (a5) is a function of
, observed from this point. The right-hand side of (a5) is a function of 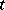 and a function of
and a function of 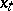 , i.e. to any function
, i.e. to any function 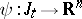 in some class of functions there corresponds a vector
in some class of functions there corresponds a vector 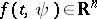 .
.
Equations (a2) and (a4) are particular cases of (a5). Similarly, the general neutral functional-differential equation can be written as
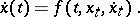 |
Various problems can be stated for functional-differential equations, e.g. the initial value problem (Cauchy problem), the boundary value problem, the existence of periodic solutions, stability, control, etc. For example, the Cauchy problem (also called the initial problem or basic initial problem) is to find the solution of the equation subjected to a given initial function and initial value. Consider the retarded functional-differential equation (a5) with finite after-effect, and let, for some 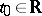 , the function
, the function 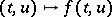 be defined for all
be defined for all 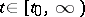 ,
, 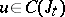 , where
, where 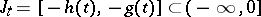 . The point
. The point 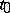 is called the initial point for the solution. Assume that
is called the initial point for the solution. Assume that
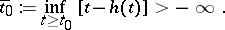 |
The initial function 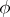 for (a5) with a prescribed initial point
for (a5) with a prescribed initial point 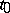 is given on the initial interval
is given on the initial interval 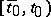 . If
. If 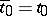 then the initial interval
then the initial interval 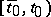 is empty and the initial function should not be prescribed. This is a Cauchy problem without previous history. Also the initial value
is empty and the initial function should not be prescribed. This is a Cauchy problem without previous history. Also the initial value 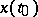 of the solution must be given.
of the solution must be given.
It is essential that the solution 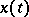 must be constructed in the direction of increasing
must be constructed in the direction of increasing  , i.e. on some interval
, i.e. on some interval 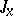 with left end
with left end 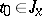 . Here,
. Here,  is considered as a prolongation of the initial function, that is,
is considered as a prolongation of the initial function, that is, 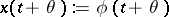 for
for 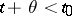 . Usually, the initial value of the solution is included in the initial function, i.e. the latter is assumed to be prescribed on the interval
. Usually, the initial value of the solution is included in the initial function, i.e. the latter is assumed to be prescribed on the interval 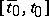 and
and 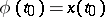 .
.
References
| [a1] | R. Bellman, K.L. Cooke, "Differential-difference equation" , Acad. Press (1963) |
| [a2] | Y. Kuang, "Delay differential equations with applications in population dynamics" , Acad. Press (1993) |
| [a3] | A.D. Myshkis, "General theory of differential equations with delay" Uspekhi Mat. Nauk , 4 : 5 (1949) pp. 99–141 |
| [a4] | A.D. Myshkis, "Lineare Differentialgleichungen mit nacheilendem Argument" , VEB (1955) (In Russian) |
| [a5] | V. Volterra, "Sulle equazioni integrodifferenziali della teorie dell' elasticita" Atti Accad. Lincei , 18 (1909) pp. 295 |
| [a6] | V. Volterra, "Théorie mathématique de la lutte pour la vie" , Gauthier-Villars (1931) |
| [a7] | C. Corduneanu, V. Lakshmikantham, "Equations with unbounded delay" Nonlinear Analysis Theory Methods Appl. , 4 : 5 (1980) pp. 831–878 |
| [a8] | K. Gopalsamy, "Equations of mathematical ecology" , Kluwer Acad. Publ. (1992) |
| [a9] | J. Hale, "Functional differential equations" , Springer (1971) |
| [a10] | J. Hale, S.M. Verduyn Lunel, "Introduction to functional differential equations" , Springer (1993) |
| [a11] | V.B. Kolmanovskii, V.R. Nosov, "Stability of functional differential equations" , Acad. Press (1986) |
| [a12] | V.B. Kolmanovskii, A.D. Myshkis, "Applied theory of functional differential equations" , Kluwer Acad. Publ. (1992) |
| [a13] | V.B. Kolmanovskii, L.E. Shaikhet, "Control of systems with aftereffect" , 157 , Amer. Math. Soc. (1997) |
| [a14] | V.B. Kolmanovskii, A.D. Myshkis, "Introduction to the theory and applications of functional differential equations" , Kluwer Acad. Publ. (1999) |
Functional-differential equation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Functional-differential_equation&oldid=15103