Function
One of the basic concepts in mathematics. Let two sets $X$ and $Y$ be given and suppose that to each element $x\in X$ corresponds an element $y\in Y$, which is denoted by $f(x)$. In this case one says that a function $f$ is given on $X$ (and also that the variable $y$ is a function of the variable $x$, or that $y$ depends on $x$) and one writes $f:X\to Y$.
In ancient mathematics the idea of functional dependence was not expressed explicitly and was not an independent object of research, although a wide range of specific functional relations were known and were studied systematically. The concept of a function appears in a rudimentary form in the works of scholars in the Middle Ages, but only in the work of mathematicians in the 17th century, and primarily in those of P. Fermat, R. Descartes, I. Newton, and G. Leibniz, did it begin to take shape as an independent concept. The term "function" first appeared in works of Leibniz. Geometric, analytic and kinematic ideas were used to specify a function, but gradually the notion of a function as a certain analytic expression began to prevail. This was formulated in the 18th century in a precise form; J. Bernoulli's definition is that "a function of a variable quantity … is a number composed by some arbitrary method from the variable quantity and from constants" . L. Euler, having accepted this definition, wrote in his textbook on analysis that "all analysis of infinitesimals revolves around the variable quantities and their functions" [1]. Euler already had a more general approach to the concept of a function as dependence of one variable quantity on another. This point of view was developed further in the work of J. Fourier, N.I. Lobachevskii, P. Dirichlet, B. Bolzano, and A.L. Cauchy, where the notion of a function as a correspondence between two sets of numbers began to crystallize. So by 1834, Lobachevskii [2] was writing: "The general concept of a function requires that a function of x is a number which is given for each x and gradually changes with x. The value of a function can be given either by an analytic expression or by a condition which gives a means of testing all numbers and choosing one of them; or finally a dependence can exist and remain unknown" . The definition of a function as a correspondence between two arbitrary sets (not necessarily consisting of numbers) was formulated by R. Dedekind in 1887 [3].
The concept of a correspondence, and consequently also the concept of a function, sometimes leads to other concepts (to a set [4], a relation [5] or some other set-theoretical or mathematico-logical concepts [6]) and is sometimes taken as a primary, undefined, concept [7]. A. Church, for example, expressed the view that: "In the end it is necessary to consider the concept of a function — or some similar concept, for example the concept of a class — as primitive or undefinable" [8]. (For more information see [9], [10].)
The concept of a function considered below is based on the concept of a set and of the simplest operations on sets.
One says that the number of elements of a set 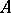 is equal to 1 or that the set
is equal to 1 or that the set  consists of one element if it contains an element
consists of one element if it contains an element  and no others (in other words, if after deleting the set
and no others (in other words, if after deleting the set 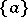 from
from 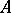 one obtains the empty set). A non-empty set
one obtains the empty set). A non-empty set 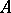 is called a set with two elements, or a pair,
is called a set with two elements, or a pair,  , if after deleting a set consisting of only one element
, if after deleting a set consisting of only one element 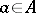 there remains a set also consisting of one element
there remains a set also consisting of one element 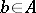 (this definition does not depend on the choice of the chosen element
(this definition does not depend on the choice of the chosen element 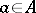 ).
).
If a pair 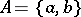 is given, then the pair
is given, then the pair 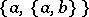 is called the ordered pair of elements
is called the ordered pair of elements 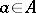 and
and 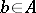 and is denoted by
and is denoted by 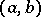 . The element
. The element 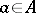 is called its first element and
is called its first element and 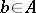 is called the second element.
is called the second element.
Given sets 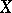 and
and 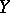 , the set of all ordered pairs
, the set of all ordered pairs  ,
, 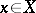 ,
, 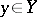 , is called the product of the sets
, is called the product of the sets 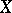 and
and 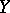 and is denoted by
and is denoted by 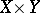 . It is not assumed that
. It is not assumed that 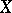 is different from
is different from 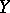 , that is, it is possible that
, that is, it is possible that 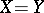 .
.
Each set 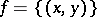 of ordered pairs
of ordered pairs 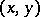 ,
,  ,
, 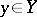 , such that, if
, such that, if 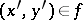 and
and  , then
, then 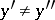 implies that
implies that 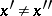 , is called a function or, what is the same thing, a mapping.
, is called a function or, what is the same thing, a mapping.
As well as the terms "function" and "mapping" one uses in certain situations the terms transformation , morphism , correspondence , which are equivalent to them.
The set of all first elements of ordered pairs 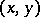 of a given function
of a given function 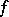 is called the domain of definition (or the set of definition) of this function and is denoted by
is called the domain of definition (or the set of definition) of this function and is denoted by 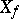 , and the set of all second elements is called the range of values (the set of values) and is denoted by
, and the set of all second elements is called the range of values (the set of values) and is denoted by 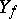 . The set of ordered pairs itself,
. The set of ordered pairs itself, 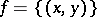 , considered as a subset of the product
, considered as a subset of the product 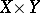 , is called the graph of
, is called the graph of 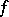 .
.
The element 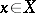 is called the argument of the function, or the independent variable, and the element
is called the argument of the function, or the independent variable, and the element 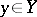 is called the dependent variable.
is called the dependent variable.
If 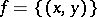 is a function, then one writes
is a function, then one writes 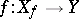 and says that
and says that 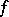 maps the set
maps the set 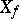 into the set
into the set 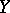 . In the case
. In the case 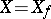 one simply writes
one simply writes 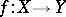 .
.
If 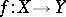 is a function and
is a function and 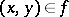 , then one writes
, then one writes 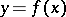 (sometimes simply
(sometimes simply 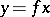 or
or 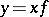 ) and also
) and also 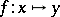 ,
, 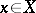 ,
, 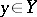 , and says that the function
, and says that the function 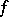 puts the element
puts the element 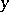 in correspondence with the element
in correspondence with the element  (the mapping
(the mapping 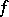 maps
maps  to
to 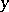 ) or, what is the same, the element
) or, what is the same, the element 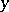 corresponds to the element
corresponds to the element  . In this case one also says that
. In this case one also says that 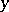 is the value of
is the value of 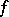 at the point
at the point  , or that
, or that 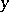 is the image of the element
is the image of the element  under
under 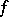 .
.
As well as the symbol 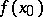 one also uses the notation
one also uses the notation 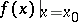 for denoting the value of
for denoting the value of 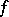 at
at 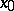 .
.
Sometimes the function 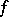 itself is denoted by the symbol
itself is denoted by the symbol 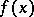 . Denoting both the function
. Denoting both the function 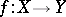 and its value at the point
and its value at the point 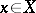 by the same symbol
by the same symbol 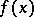 does not usually lead to misunderstanding, since in any particular case, as a rule, it is always clear what one is talking about. The notation
does not usually lead to misunderstanding, since in any particular case, as a rule, it is always clear what one is talking about. The notation 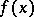 often turns out to be more convenient than the notation
often turns out to be more convenient than the notation 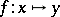 in computations. For example, writing
in computations. For example, writing  is more convenient and simpler to use in analytic manipulations than writing
is more convenient and simpler to use in analytic manipulations than writing 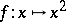 .
.
Given 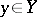 , the set of all elements
, the set of all elements  such that
such that 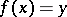 is called the pre-image of the element
is called the pre-image of the element 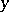 and is denoted by
and is denoted by 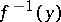 . Thus,
. Thus,
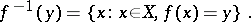 |
Obviously, if 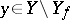 , then
, then 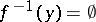 , the empty set.
, the empty set.
Let a mapping 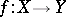 be given. In other words, to each
be given. In other words, to each 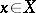 corresponds a unique element
corresponds a unique element 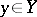 and to each
and to each 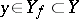 corresponds at least one element
corresponds at least one element 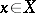 . If
. If 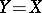 , one says that
, one says that  maps the set
maps the set 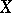 into itself. If
into itself. If 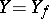 , that is, if
, that is, if 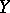 coincides with the range of
coincides with the range of 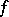 , then one says that
, then one says that 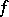 maps
maps 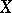 onto the set
onto the set 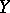 or that
or that  is a surjective mapping, or, more concisely, it is a surjection. Thus, a mapping
is a surjective mapping, or, more concisely, it is a surjection. Thus, a mapping 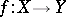 is a surjection if for each element
is a surjection if for each element 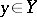 there is at least one element
there is at least one element 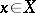 such that
such that 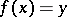 .
.
If under a mapping 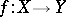 different elements
different elements 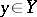 correspond to different elements
correspond to different elements 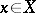 , that is, if
, that is, if 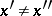 implies
implies 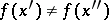 , then
, then 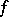 is said to be a one-to-one mapping of
is said to be a one-to-one mapping of 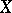 into
into 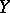 and also a univalent mapping or an injection. Thus, a mapping
and also a univalent mapping or an injection. Thus, a mapping 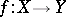 is univalent (injective) if and only if the pre-image of each element
is univalent (injective) if and only if the pre-image of each element 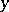 belonging to the range of
belonging to the range of 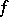 , that is,
, that is,  , consists precisely of one element. If the mapping
, consists precisely of one element. If the mapping 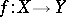 is simultaneously one-to-one and onto the set
is simultaneously one-to-one and onto the set 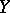 (see One-to-one correspondence), that is, is at the same time injective and surjective, then it is called a bijective mapping or a bijection.
(see One-to-one correspondence), that is, is at the same time injective and surjective, then it is called a bijective mapping or a bijection.
If 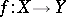 and
and 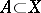 , then the set
, then the set
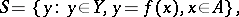 |
that is, the set of all those 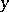 such that there is at least one element of the subset
such that there is at least one element of the subset 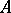 of
of 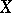 which is mapped to
which is mapped to 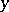 by
by 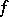 , is called the image of the subset
, is called the image of the subset 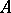 , and one writes
, and one writes 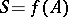 . In particular, always
. In particular, always 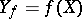 . The following relations are true for the images of sets
. The following relations are true for the images of sets 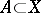 and
and 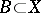 :
:
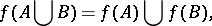 |
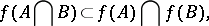 |
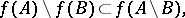 |
and if 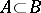 , then
, then 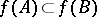 .
.
If 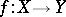 and
and 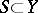 , then the set
, then the set
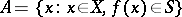 |
is called the pre-image of the set 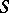 and one writes
and one writes 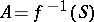 . Thus, the pre-image of a set
. Thus, the pre-image of a set 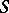 consists of all those elements
consists of all those elements 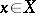 which are mapped to elements of
which are mapped to elements of 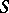 under
under 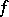 , or what is the same thing, it consists of all pre-images of elements
, or what is the same thing, it consists of all pre-images of elements 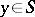 :
: 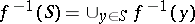 . For the pre-images of sets
. For the pre-images of sets 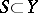 and
and 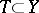 the relations
the relations
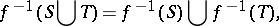 |
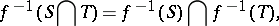 |
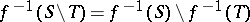 |
are true, and if 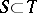 , then
, then 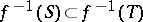 .
.
If 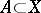 , then the function
, then the function 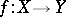 generates in a natural way a function defined on
generates in a natural way a function defined on 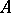 under which
under which 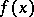 corresponds to the element
corresponds to the element  . This function is called the restriction of the function
. This function is called the restriction of the function 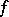 to the set
to the set 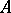 and is sometimes denoted by
and is sometimes denoted by 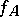 . Thus
. Thus 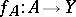 and for any
and for any 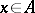 one has
one has 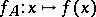 . If the set
. If the set 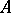 does not coincide with the set
does not coincide with the set 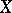 , then the restriction
, then the restriction 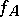 of
of 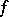 to
to 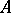 may have a different domain of definition than
may have a different domain of definition than 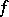 and, consequently, is different from
and, consequently, is different from 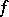 .
.
If 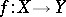 , if each element
, if each element 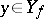 is a certain set of elements
is a certain set of elements 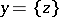 , and if, moreover, among these sets there is at least one set consisting of more than one element, then
, and if, moreover, among these sets there is at least one set consisting of more than one element, then 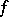 is called a multi-valued function (sometimes, many-valued function). Further, the elements of the set
is called a multi-valued function (sometimes, many-valued function). Further, the elements of the set 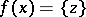 are often called the values of
are often called the values of 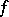 at
at  . If each set
. If each set 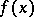 ,
, 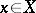 , consists of only one element, then the function
, consists of only one element, then the function 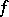 is also called a single-valued function.
is also called a single-valued function.
If 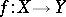 and
and 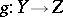 , then the function
, then the function 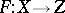 defined for each
defined for each 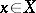 by the formula
by the formula 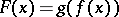 is called the composition (superposition) of the functions
is called the composition (superposition) of the functions 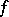 and
and 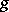 , also the composite function, and is denoted by
, also the composite function, and is denoted by 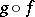 .
.
Let a function 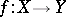 be given and let
be given and let 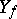 be its range. The set of all possible ordered pairs of the form
be its range. The set of all possible ordered pairs of the form 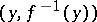 ,
, 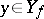 , forms a function, called the inverse function of
, forms a function, called the inverse function of 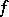 and denoted by
and denoted by 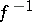 . Under the inverse function
. Under the inverse function 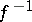 , to each
, to each 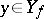 corresponds the pre-image
corresponds the pre-image 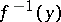 , that is, a certain set of elements. So the inverse function is, generally speaking, a multi-valued function. If a mapping
, that is, a certain set of elements. So the inverse function is, generally speaking, a multi-valued function. If a mapping 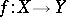 is injective, then the inverse mapping is a single-valued function and maps the range
is injective, then the inverse mapping is a single-valued function and maps the range 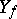 of
of 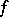 onto the domain of definition
onto the domain of definition 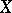 of
of 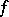 .
.
Functions on numbers.
An important class of functions is that of the complex-valued functions 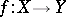 ,
, 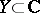 , where
, where  is the set of all complex numbers. One can carry out various arithmetical operations on complex-valued functions. If two given complex-valued functions
is the set of all complex numbers. One can carry out various arithmetical operations on complex-valued functions. If two given complex-valued functions  and
and 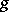 are defined on the same set
are defined on the same set 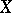 and if
and if 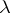 is a complex number, then the function
is a complex number, then the function 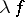 is defined as the function taking the value
is defined as the function taking the value 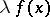 at each point
at each point 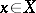 ; the function
; the function 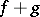 is the function taking the value
is the function taking the value 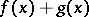 at each point; the function
at each point; the function 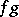 is the function taking the value
is the function taking the value 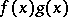 at each point; and, finally,
at each point; and, finally, 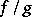 is the function equal to
is the function equal to 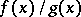 at each point
at each point 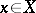 (which, of course, makes sense only when
(which, of course, makes sense only when 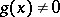 ).
).
A function 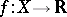 is called a real-valued function (
is called a real-valued function (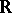 is the set of real numbers). A real-valued function
is the set of real numbers). A real-valued function 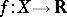 is said to be bounded from above (bounded from below) on the set
is said to be bounded from above (bounded from below) on the set 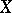 if its range is bounded from above (bounded from below). In other words, a function
if its range is bounded from above (bounded from below). In other words, a function 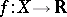 is bounded from above (bounded from below) on
is bounded from above (bounded from below) on 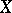 if there is a constant
if there is a constant 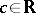 such that for every
such that for every 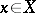 the inequality
the inequality 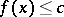 is satisfied (the inequality
is satisfied (the inequality 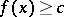 is satisfied, respectively). A function
is satisfied, respectively). A function 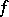 that is both bounded from above and from below on
that is both bounded from above and from below on 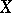 is simply said to be bounded on
is simply said to be bounded on 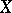 . An upper (lower) bound of the range of
. An upper (lower) bound of the range of 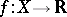 is an upper (lower) bound of the function
is an upper (lower) bound of the function 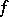 .
.
A major role in mathematical analysis is played by functions on numbers or, more precisely, complex-valued functions of a complex variable, that is, functions 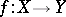 , where
, where 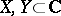 . If the domain of definition of such a function and its range are both subsets of the real numbers, then this function is called a real function, or, more precisely, a real-valued function of a real variable. The generalization of the concept of a function on numbers is, first of all, a complex-valued function of several complex variables, called a complex function of several variables. A further generalization of a function on numbers is a vector-valued function (see Vector function) and, in general, a function for which the domain of definition and the range are provided with definite structures. For example, if the ranges of functions belong to a certain vector space, then such functions can be added; if they belong to a ring, then the functions can be added and multiplied; if they belong to a set which is ordered in some specific way, then one can generalize to these functions the idea of boundedness, upper and lower bounds, etc. The presence of topological structures on the sets
. If the domain of definition of such a function and its range are both subsets of the real numbers, then this function is called a real function, or, more precisely, a real-valued function of a real variable. The generalization of the concept of a function on numbers is, first of all, a complex-valued function of several complex variables, called a complex function of several variables. A further generalization of a function on numbers is a vector-valued function (see Vector function) and, in general, a function for which the domain of definition and the range are provided with definite structures. For example, if the ranges of functions belong to a certain vector space, then such functions can be added; if they belong to a ring, then the functions can be added and multiplied; if they belong to a set which is ordered in some specific way, then one can generalize to these functions the idea of boundedness, upper and lower bounds, etc. The presence of topological structures on the sets 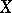 and
and 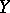 enables one to introduce the concept of a continuous function
enables one to introduce the concept of a continuous function 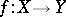 . In the case when
. In the case when 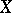 and
and 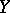 are topological vector spaces one introduces the concept of differentiability for a function
are topological vector spaces one introduces the concept of differentiability for a function 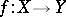 (cf. Differentiable function).
(cf. Differentiable function).
Methods for specifying functions.
Functions on numbers (and certain generalizations of them) can be given by formulas. This is the analytic method for specifying functions. For this one uses a certain supply of functions which have been studied and have a special notation (primarily the elementary functions), algebraic operations, composition of functions and limit transitions (which includes operations of mathematical analysis such as differentiation, integration, summing series), for example:
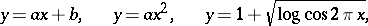 |
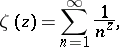 |
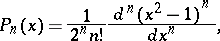 |
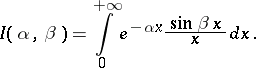 |
The class of functions that are presented, in a well-determined sense, as the sum of series, even only as sums of trigonometric series, is very wide. A function can be given analytically either in an explicit form, that is, by a formula of the type 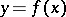 , or as an implicit function, that is, by an equation of the type
, or as an implicit function, that is, by an equation of the type 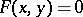 . Sometimes the function is given with the aid of several formulas, for example,
. Sometimes the function is given with the aid of several formulas, for example,
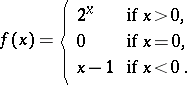 | (*) |
A function can also be given by using a description of the correspondence. Let, for example, the number 1 correspond to every 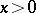 , the number 0 to the number 0, and the number
, the number 0 to the number 0, and the number 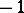 to every
to every 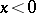 . As a result one obtains a function defined on the whole real line and taking three values:
. As a result one obtains a function defined on the whole real line and taking three values: 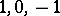 . This function has the special notation
. This function has the special notation 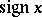 (or
(or 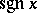 ). Another example: the number 1 corresponds to each rational number and the number 0 to each irrational number. The function obtained is called the Dirichlet function. The same function can be given in different ways; for example, the function
). Another example: the number 1 corresponds to each rational number and the number 0 to each irrational number. The function obtained is called the Dirichlet function. The same function can be given in different ways; for example, the function 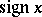 and the Dirichlet function can be defined not only by verbal descriptions but also by formulas.
and the Dirichlet function can be defined not only by verbal descriptions but also by formulas.
Every formula is a symbolic notation of a certain previously-described correspondence, so that in the end there is no fundamental difference between specifying a function by a formula or by a verbal description of the correspondence; this difference is superficial. It should be borne in mind that every function newly defined by some means or other can, if a special notation is introduced for it, serve to define other functions by using formulas including this new symbol. However, for an analytic representation of a function the supply of functions and operations that are to be used in the formulas is very essential; usually one tries to make this supply as small as possible and chooses the functions and operations as simply as possible in a certain well-determined sense.
When one is concerned with real-valued functions of a single real variable, then to give an intuitive representation of the nature of the functional dependence one often constructs the graph of the function in the coordinate plane, in other words, given a function 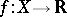 ,
, 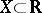 , one considers the set of points
, one considers the set of points 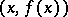 ,
, 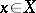 , in the
, in the 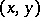 -plane.
-plane. 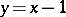
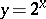
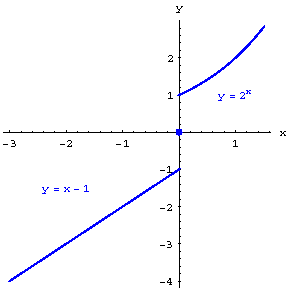
Figure: f041940a
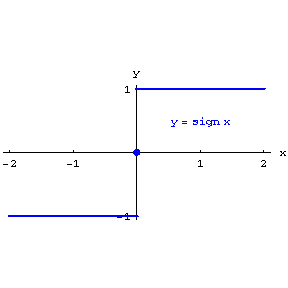
Figure: f041940b
Thus, the graph of the function (*) has the form depicted in Fig. a, the graph of the function 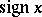 is Fig. b, and the graph of the function
is Fig. b, and the graph of the function 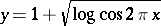 consists of the isolated points in Fig. c.
consists of the isolated points in Fig. c.
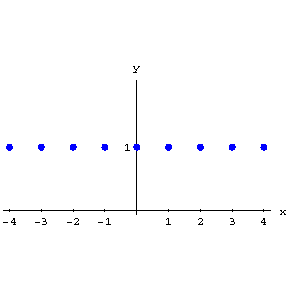
Figure: f041940c
The representation of a function by a graph can also serve to reveal a functional dependence. This revelation is approximate because, in practice, the measurement of the intervals can be carried out only with a definite degree of accuracy, without mentioning the fact that, when the domain of definition of the function is unbounded, it is in principle impossible to draw it on the coordinate plane.
A tabular method is also extensively used for representing functions on numbers, either in the form of prepared tables of values of the function at definite points, or by introducing this data into a machine memory, or by making a program to calculate the values on a computer.
The classification of complex or real functions.
The simplest complex functions are the elementary functions, among which one distinguishes the algebraic polynomials, the trigonometric polynomials and also the rational functions (cf. Rational function). The special role of these functions is that one of the methods for studying and using more general functions is based on approximating them by algebraic polynomials, by trigonometric polynomials or by rational functions, as well as by functions composed from these functions in some well-determined way (see Spline). The branch of the theory of functions that studies the approximation of functions by collections of functions that are simple in a certain sense is called approximation theory. In this theory approximations of functions by linear aggregates of eigen functions of certain operators are also very important.
The analytic functions (cf. Analytic function), i.e. functions locally representable by power series, form an important class, containing the rational functions. The analytic functions can be subdivided into the algebraic functions (cf. Algebraic function), that is, functions 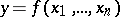 that can be given by an equation
that can be given by an equation 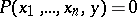 , where
, where 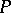 is an irreducible polynomial with complex coefficients, and transcendental functions, that is, those which are not algebraic. With the concept of a derivative one can associate the classes of functions that are differentiable a definite number of times, with the concept of an integral one can associate the classes of functions that are integrable in some sense or other, and with the concept of continuity one can associate the class of continuous functions. The Baire classes of functions are obtained by taking successive pointwise limits from the class of continuous functions (see also Borel function). The definition of a measurable function is based on the concepts of a measurable set and a measure. The branch of the theory of functions that studies properties of functions associated with the concept of a measure is usually called the metric theory of functions.
is an irreducible polynomial with complex coefficients, and transcendental functions, that is, those which are not algebraic. With the concept of a derivative one can associate the classes of functions that are differentiable a definite number of times, with the concept of an integral one can associate the classes of functions that are integrable in some sense or other, and with the concept of continuity one can associate the class of continuous functions. The Baire classes of functions are obtained by taking successive pointwise limits from the class of continuous functions (see also Borel function). The definition of a measurable function is based on the concepts of a measurable set and a measure. The branch of the theory of functions that studies properties of functions associated with the concept of a measure is usually called the metric theory of functions.
A function space arises as a collection of functions having certain general properties. Thus, all functions defined on the same set 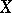 in the
in the  -dimensional Euclidean space
-dimensional Euclidean space 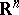 and, for example, Lebesgue measurable, continuous, or satisfying a Hölder condition of given order, respectively, form vector spaces. Similarly, the spaces of
and, for example, Lebesgue measurable, continuous, or satisfying a Hölder condition of given order, respectively, form vector spaces. Similarly, the spaces of 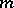 times (continuously-) differentiable functions,
times (continuously-) differentiable functions, 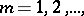 the infinitely-differentiable functions, the functions of compact support, the analytic functions, and many other classes of functions form vector spaces.
the infinitely-differentiable functions, the functions of compact support, the analytic functions, and many other classes of functions form vector spaces.
In a number of vector spaces of functions one can introduce a norm. For example, in the space of continuous functions on a compact space 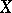 ,
,  , a norm is
, a norm is 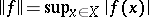 ; the normed space of continuous functions with this norm is denoted by
; the normed space of continuous functions with this norm is denoted by 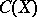 . Given the space of measurable functions
. Given the space of measurable functions 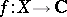 , defined on a space
, defined on a space 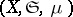 , where
, where 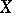 is a certain set,
is a certain set, 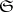 is a certain
is a certain 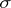 -algebra of subsets of
-algebra of subsets of 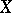 and
and 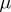 is a measure defined on the sets
is a measure defined on the sets 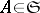 , by putting
, by putting
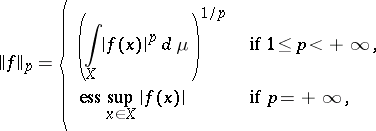 |
one specifies a norm 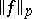 on the set of functions for which
on the set of functions for which 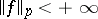 . A function space with such a norm is usually called a Lebesgue function space
. A function space with such a norm is usually called a Lebesgue function space 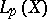 . Among the other function spaces playing an important role in mathematical analysis one should mention a Hölder space, a Nikol'skii space, an Orlicz space, and a Sobolev space. All these spaces and certain generalizations of them are complete metric spaces, which to a large extent is important in studying many problems in the theory of functions itself as well as problems from related branches of mathematics. The relations between various norms for functions belonging simultaneously to various function spaces are studied in the theory of imbedding of function spaces (see Imbedding theorems). An important property of the basic function spaces is that the set of infinitely-differentiable functions is dense in them, which enables one to study a number of properties of these function spaces on sufficiently-smooth functions, and to carry over the results to all functions in the space under consideration by taking limits.
. Among the other function spaces playing an important role in mathematical analysis one should mention a Hölder space, a Nikol'skii space, an Orlicz space, and a Sobolev space. All these spaces and certain generalizations of them are complete metric spaces, which to a large extent is important in studying many problems in the theory of functions itself as well as problems from related branches of mathematics. The relations between various norms for functions belonging simultaneously to various function spaces are studied in the theory of imbedding of function spaces (see Imbedding theorems). An important property of the basic function spaces is that the set of infinitely-differentiable functions is dense in them, which enables one to study a number of properties of these function spaces on sufficiently-smooth functions, and to carry over the results to all functions in the space under consideration by taking limits.
Dependence of functions.
This is a property of systems of functions generalizing the concept of their linear dependence and meaning that there are well-determined relations between the values of the functions in the given system; in particular, the values of one of them can be expressed in terms of the values of the others. For example, the functions 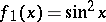 and
and 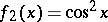 are dependent over the whole real line, since always
are dependent over the whole real line, since always 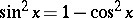 . Let
. Let 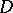 be a domain in
be a domain in 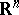 , let
, let 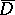 be its closure and let
be its closure and let 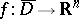 ,
, 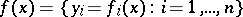 ,
, 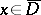 . The functions
. The functions 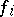 ,
,  , are said to be dependent in
, are said to be dependent in 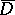 if there is a continuously-differentiable function
if there is a continuously-differentiable function 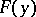 ,
,  , whose zeros form a nowhere-dense set in
, whose zeros form a nowhere-dense set in 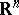 and such that the composite
and such that the composite 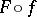 is identically zero on
is identically zero on 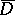 .
.
Functions 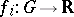 ,
, 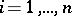 , are said to be dependent in the domain
, are said to be dependent in the domain 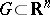 if they are dependent in the closure
if they are dependent in the closure 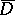 of any domain
of any domain 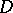 such that
such that 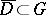 .
.
Functions 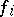 ,
, 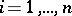 , that are continuously differentiable in a domain
, that are continuously differentiable in a domain 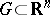 are dependent in
are dependent in 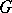 if and only if their Jacobian
if and only if their Jacobian
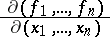 |
vanishes identically on 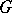 .
.
Now let
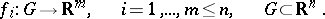 | (1) |
If for 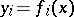 ,
, 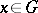 ,
, 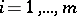 ,
, 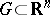 , there is an open set
, there is an open set 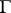 in
in  and a continuously-differentiable function
and a continuously-differentiable function 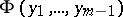 on
on 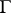 such that at any point
such that at any point  ,
,
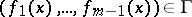 |
and
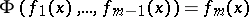 |
are satisfied, then 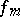 is said to be dependent in the set
is said to be dependent in the set 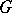 on the functions
on the functions 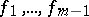 .
.
If the functions 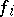 ,
, 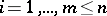 , are continuous in a domain
, are continuous in a domain 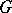 and if in a neighbourhood of each point
and if in a neighbourhood of each point 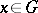 one of them depends on the others, then the functions
one of them depends on the others, then the functions 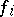 ,
, 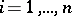 , are dependent in
, are dependent in 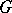 .
.
If in a neighbourhood of each point 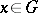 one of the functions
one of the functions 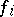 ,
, 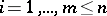 , which are continuously-differentiable in a domain
, which are continuously-differentiable in a domain 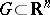 , depends on the others, then at any point of
, depends on the others, then at any point of 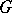 the rank of the Jacobi matrix
the rank of the Jacobi matrix
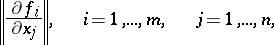 | (2) |
is less than 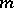 , that is, the gradients
, that is, the gradients  are linearly dependent at each point
are linearly dependent at each point 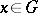 .
.
Let the functions (1) be continuously differentiable in a domain 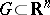 and let the rank of their Jacobi matrix (2) not exceed a certain number
and let the rank of their Jacobi matrix (2) not exceed a certain number  ,
, 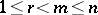 , at every point
, at every point 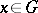 ; suppose, moreover, that at a certain point
; suppose, moreover, that at a certain point 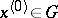 it is equal to
it is equal to  . In other words, there are variables
. In other words, there are variables  and functions
and functions 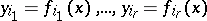 such that
such that
 | (3) |
Then there is no neighbourhood of 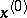 in which any of the functions
in which any of the functions 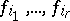 depends on the others and there is a neighbourhood of
depends on the others and there is a neighbourhood of 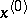 such that each of the remaining functions
such that each of the remaining functions 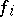 ,
, 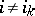 ,
, 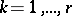 , depends in this neighbourhood on
, depends in this neighbourhood on  . In particular, if the gradients
. In particular, if the gradients 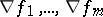 are linearly dependent at all points of the domain
are linearly dependent at all points of the domain 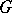 and if at a certain point
and if at a certain point 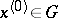 there are
there are 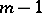 of them that are linearly independent, and consequently one of them, for example
of them that are linearly independent, and consequently one of them, for example 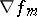 , is a linear combination of the others, then there is a neighbourhood of
, is a linear combination of the others, then there is a neighbourhood of 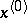 such that in this neighbourhood
such that in this neighbourhood 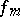 depends on the functions
depends on the functions 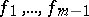 .
.
References
| [1] | L. Euler, "Einleitung in die Analysis des Unendlichen" , 1 , Springer (1983) (Translated from Latin) |
| [2] | N.I. Lobachevskii, "Complete works" , 5 , Moscow-Leningrad (1951) (In Russian) |
| [3] | R. Dedekind, "The nature and meaning of numbers" , Open Court (1901) (Translated from German) |
| [4] | F. Hausdorff, "Grundzüge der Mengenlehre" , Leipzig (1914) (Reprinted (incomplete) English translation: Set theory, Chelsea (1978)) |
| [5] | A. Tarski, "Introduction to logic and to the methodology of deductive sciences" , Oxford Univ. Press (1946) (Translated from German) |
| [6] | K. Kuratowski, "Topology" , 1 , PWN & Acad. Press (1966) (Translated from French) |
| [7] | G. Frege, "Funktion und Begriff" , H. Pohle (1891) ((Reprint: Kleine Schriften, G. Olms, 1967)) |
| [8] | A. Church, "Introduction to mathematical logic" , 1 , Princeton Univ. Press (1956) |
| [9] | A.P. Yushkevich, "The concept of function up to the middle of the nineteenth century" Arch. History of Exact Sci. , 16 (1977) pp. 37–85 Istor.-Mat. Issled. , 17 (1966) pp. 123–150 |
| [10] | F.A. Medvedev, "Outlines of the history of the theory of functions of a real variable" , Moscow (1975) (In Russian) |
Comments
A pre-image is also called an inverse image. The restriction of a function 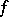 to a set
to a set 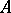 is generally denoted by
is generally denoted by 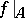 or
or 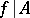 ; in axiomatic set theory, the image
; in axiomatic set theory, the image 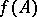 is always written
is always written 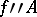 in order to avoid any misunderstanding. Strictly speaking, the definition of a many-valued function in the article doesn't make sense: in fact, a function
in order to avoid any misunderstanding. Strictly speaking, the definition of a many-valued function in the article doesn't make sense: in fact, a function 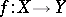 where
where 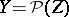 (the set of subsets of
(the set of subsets of 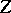 ) is called a many-valued function
) is called a many-valued function 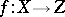 . Finally, the phrase metric theory of functions is not often used in the West; there is no generally accepted name for this area of research.
. Finally, the phrase metric theory of functions is not often used in the West; there is no generally accepted name for this area of research.
References
| [a1] | S. MacLane, "Mathematics, form and function" , Springer (1986) |
| [a2] | H.L. Royden, "Real analysis", Macmillan (1968) pp. Chapt. 5 |
| [a3] | A.C.M. van Rooy, W.H. Schikhof, "A second course on real functions" , Cambridge Univ. Press (1982) |
| [a4] | B.R. Gelbaum, J.M.H. Olmsted, "Counterexamples in analysis" , Holden-Day (1964) |
Function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Function&oldid=44361