Fubini theorem
A theorem that establishes a connection between a multiple integral and a repeated one. Suppose that  and
and 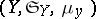 are measure spaces with
are measure spaces with  -finite complete measures
-finite complete measures 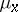 and
and 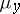 defined on the
defined on the 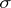 -algebras
-algebras 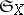 and
and  , respectively. If the function
, respectively. If the function 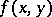 is integrable on the product
is integrable on the product 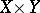 of
of 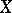 and
and 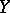 with respect to the product measure
with respect to the product measure 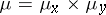 of
of 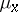 and
and 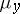 , then for almost-all
, then for almost-all 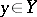 the function
the function 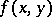 of the variable
of the variable  is integrable on
is integrable on 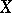 with respect to
with respect to  , the function
, the function 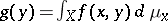 is integrable on
is integrable on 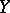 with respect to
with respect to 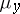 , and one has the equality
, and one has the equality
 | (1) |
Fubini's theorem is valid, in particular, for the case when 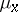 ,
, 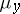 and
and 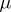 are the Lebesgue measures in the Euclidean spaces
are the Lebesgue measures in the Euclidean spaces 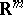 ,
,  and
and  respectively (
respectively (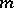 and
and  are natural numbers),
are natural numbers),  ,
, 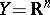 ,
,  , and
, and 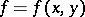 is a Lebesgue-measurable function on
is a Lebesgue-measurable function on  ,
, 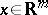 ,
, 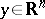 . Under these assumptions, formula (1) has the form
. Under these assumptions, formula (1) has the form
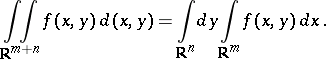 | (2) |
In the case of a function 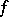 defined on an arbitrary Lebesgue-measurable set
defined on an arbitrary Lebesgue-measurable set 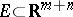 , in order to express the multiple integral in terms of a repeated one, one must extend
, in order to express the multiple integral in terms of a repeated one, one must extend 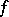 by zero to the whole of
by zero to the whole of 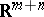 and apply (2). See also Repeated integral.
and apply (2). See also Repeated integral.
The theorem was established by G. Fubini [1].
References
| [1] | G. Fubini, "Sugli integrali multipli" , Opere scelte , 2 , Cremonese (1958) pp. 243–249 |
Fubini theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fubini_theorem&oldid=17242