Freiheitssatz
independence theorem
A theorem originally proposed by M. Dehn in a geometrical setting and originally proven by W. Magnus [a1]. This theorem is the cornerstone of one-relator group theory.
The Freiheitssatz says the following: Let  be a group defined by a single cyclically reduced relator
be a group defined by a single cyclically reduced relator  . If
. If  appears in
appears in  , then the subgroup of
, then the subgroup of  generated by
generated by  is a free group, freely generated by
is a free group, freely generated by  .
.
In coarser language, the theorem says that if  is as above, then the only relations in
is as above, then the only relations in  are the trivial ones.
are the trivial ones.
The Freiheitssatz can be considered as a non-commutative analogue of certain more transparent results in commutative algebra. For example, suppose that 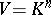 is a linear space over a field
is a linear space over a field 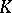 with a basis
with a basis  . If
. If 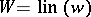 is the subspace of
is the subspace of 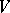 generated by a vector
generated by a vector 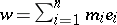 with
with 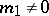 , then the elements
, then the elements  are linearly independent modulo
are linearly independent modulo 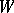 .
.
Magnus' method of proof of the Freiheitssatz relies on amalgamations (cf. also Amalgam; Amalgam of groups). This method initiated the use of these products in the study of infinite discrete groups.
One of the by-products of Magnus' proof was an extraordinary description of the structure of these groups, which allowed him to deduce that one-relator groups have solvable word problem (cf. also Identity problem; [a2]).
There are two general approaches to extending the Freiheitssatz. The first is concerned with the notion of the one-relator product 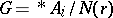 of a family
of a family 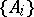 of groups, where the element
of groups, where the element  is cyclically reduced and of syllable length at least
is cyclically reduced and of syllable length at least  and
and 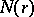 is its normal closure in
is its normal closure in 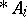 . Some authors (see [a3]) give conditions for the factors
. Some authors (see [a3]) give conditions for the factors  to inject into
to inject into 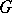 .
.
The second approach is concerned with multi-relator versions of the Freiheitssatz (see [a3] for a list of references). For example, the following strong result by N.S. Romanovskii [a4] holds: Let 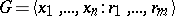 have deficiency
have deficiency  . Then there exist a subset of
. Then there exist a subset of  of the given generators which freely generates a subgroup of
of the given generators which freely generates a subgroup of  .
.
References
| [a1] | W. Magnus, "Über discontinuierliche Gruppen mit einer definierenden Relation (Der Freiheitssatz)" J. Reine Angew. Math. , 163 (1930) pp. 141–165 |
| [a2] | W. Magnus, "Das Identitätsproblem für Gruppen mit einer definierenden Relation" Math. Ann. , 106 (1932) pp. 295–307 |
| [a3] | B. Fine, G. Rosenberger, "The Freiheitssatz and its extensions" Contemp. Math. , 169 (1994) pp. 213–252 |
| [a4] | N.S. Romanovskii, "Free subgroups of finitely presented groups" Algebra i Logika , 16 (1977) pp. 88–97 (In Russian) |
Freiheitssatz. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Freiheitssatz&oldid=16698