Free algebra
in a class  of universal algebras
of universal algebras
An algebra  in
in  with a free generating system (or base)
with a free generating system (or base)  , that is, with a set
, that is, with a set  of generators such that every mapping of
of generators such that every mapping of  into any algebra
into any algebra  from
from  can be extended to a homomorphism of
can be extended to a homomorphism of  into
into  (see Free algebraic system). Any non-empty class of algebras that is closed under subalgebras and direct products and that contains non-singleton algebras, has free algebras. In particular, free algebras always exist in non-trivial varieties and quasi-varieties of universal algebras (see Variety of universal algebras; Algebraic systems, quasi-variety of). A free algebra in the class of all algebras of a given signature
(see Free algebraic system). Any non-empty class of algebras that is closed under subalgebras and direct products and that contains non-singleton algebras, has free algebras. In particular, free algebras always exist in non-trivial varieties and quasi-varieties of universal algebras (see Variety of universal algebras; Algebraic systems, quasi-variety of). A free algebra in the class of all algebras of a given signature  is called absolutely free. An algebra
is called absolutely free. An algebra  of signature
of signature  is a free algebra in some class of universal algebras of signature
is a free algebra in some class of universal algebras of signature  if and only if
if and only if  is intrinsically free, that is, if it has a generating set
is intrinsically free, that is, if it has a generating set  such that every mapping of
such that every mapping of  into
into  can be extended to an endomorphism of
can be extended to an endomorphism of  . If a free algebra has an infinite base, then all its bases have the same cardinality (see Free Abelian group; Free algebra over a ring; Free associative algebra; Free Boolean algebra; Free group; Free semi-group; Free lattice; Free groupoid; Free module; and also Free product). Clearly, every element of a free algebra with a base
. If a free algebra has an infinite base, then all its bases have the same cardinality (see Free Abelian group; Free algebra over a ring; Free associative algebra; Free Boolean algebra; Free group; Free semi-group; Free lattice; Free groupoid; Free module; and also Free product). Clearly, every element of a free algebra with a base  can be written as a word over the alphabet
can be written as a word over the alphabet 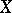 in the signature of the class being considered. It is natural to ask: When are different words equal as elements of the free algebra? In certain cases the answer is almost trivial (semi-groups, rings, groups, associative algebras), while in others it is fairly complicated (Lie algebras, lattices, Boolean algebras), and sometimes it does not have a recursive solution (alternative rings).
in the signature of the class being considered. It is natural to ask: When are different words equal as elements of the free algebra? In certain cases the answer is almost trivial (semi-groups, rings, groups, associative algebras), while in others it is fairly complicated (Lie algebras, lattices, Boolean algebras), and sometimes it does not have a recursive solution (alternative rings).
Comments
Sometimes the phrases "free algebra" and "free algebraic system" are identified in meaning. See Free algebraic system.
Free algebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Free_algebra&oldid=12553