Fredholm solvability
Let 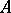 be a real
be a real 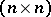 -matrix and
-matrix and  a vector.
a vector.
The Fredholm alternative in  states that the equation
states that the equation  has a solution if and only if
has a solution if and only if  for every vector
for every vector  satisfying
satisfying  .
.
This alternative has many applications, e.g. in bifurcation theory. It can be generalized to abstract spaces. So, let 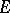 and
and 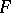 be Banach spaces (cf. Banach space) and let
be Banach spaces (cf. Banach space) and let 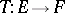 be a continuous linear operator. Let
be a continuous linear operator. Let 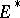 , respectively
, respectively 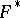 , denote the topological dual of
, denote the topological dual of  , respectively
, respectively 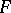 , and let
, and let 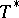 denote the adjoint of
denote the adjoint of 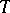 (cf. also Duality; Adjoint operator). Define
(cf. also Duality; Adjoint operator). Define
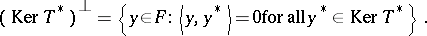 |
An equation 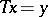 is said to be normally solvable (in the sense of F. Hausdorff) if it has a solution whenever
is said to be normally solvable (in the sense of F. Hausdorff) if it has a solution whenever 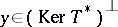 (cf. also Normal solvability). A classical result states that
(cf. also Normal solvability). A classical result states that 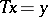 is normally solvable if and only if
is normally solvable if and only if 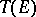 is closed in
is closed in 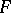 .
.
In non-linear analysis, this latter result is used as definition of normal solvability for non-linear operators.
The phrase "Fredholm solvability" refers to results and techniques for solving differential and integral equations via the Fredholm alternative and, more generally, Fredholm-type properties of the operator involved.
References
| [a1] | F. Hausdorff, "Zur Theorie der linearen metrischen Räume" J. Reine Angew. Math. , 167 (1932) pp. 265 |
| [a2] | V.A. Kozlov, V.G. Maz'ya, J. Rossmann, "Elliptic boundary value problems in domains with point singularities" , Amer. Math. Soc. (1997) |
| [a3] | A.T. Prilepko, D.G. Orlovsky, I.A. Vasin, "Methods for solving inverse problems in mathematical physics" , M. Dekker (2000) |
| [a4] | D.G. Orlovskij, "The Fredholm solvability of inverse problems for abstract differential equations" A.N. Tikhonov (ed.) et al. (ed.) , Ill-Posed Problems in the Natural Sciences , VSP (1992) |
Fredholm solvability. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fredholm_solvability&oldid=14350