Franklin system
One of the classical orthonormal systems of continuous functions. The Franklin system 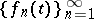 (see [1] or [2]) is obtained by applying the Schmidt orthogonalization process (cf. Orthogonalization method) on the interval
(see [1] or [2]) is obtained by applying the Schmidt orthogonalization process (cf. Orthogonalization method) on the interval 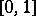 to the Faber–Schauder system, which is constructed using the set of all dyadic rational points in
to the Faber–Schauder system, which is constructed using the set of all dyadic rational points in 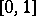 ; in this case the Faber–Schauder system is, up to constant multiples, the same as the system
; in this case the Faber–Schauder system is, up to constant multiples, the same as the system 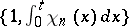 , where
, where 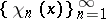 is the Haar system. The Franklin system was historically the first example of a basis in the space of continuous functions that had the property of orthogonality. This system is also a basis in all the spaces
is the Haar system. The Franklin system was historically the first example of a basis in the space of continuous functions that had the property of orthogonality. This system is also a basis in all the spaces 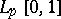 ,
, 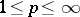 (see [3]). If a continuous function
(see [3]). If a continuous function 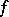 on
on  has modulus of continuity
has modulus of continuity 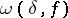 , and
, and 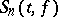 is the partial sum of order
is the partial sum of order  of the Fourier series of
of the Fourier series of 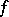 with respect to the Franklin system, then
with respect to the Franklin system, then
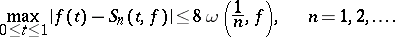 |
Here the Fourier–Franklin coefficients 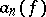 of
of 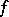 satisfy the inequalities
satisfy the inequalities
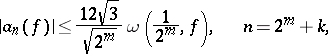 |
 |
and the conditions
a) 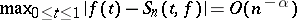 ,
, 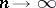 ;
;
b) 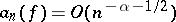 ,
, 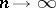 ;
;
c) 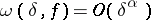 ,
, 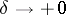 ; are equivalent for
; are equivalent for 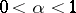 .
.
If the continuous function  is such that
is such that
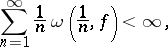 |
then the series
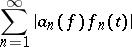 |
converges uniformly on 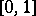 , and if
, and if
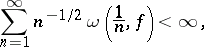 |
then
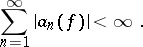 |
All these properties of the Franklin system are proved by using the inequalities
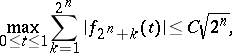 |
 |
The Franklin system is an unconditional basis in all the spaces 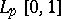
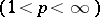 and, moreover, in all reflexive Orlicz spaces (see [5]). If
and, moreover, in all reflexive Orlicz spaces (see [5]). If 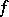 belongs to
belongs to 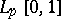 ,
, 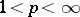 , then one has the inequality
, then one has the inequality
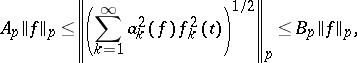 |
where 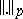 denotes the norm in
denotes the norm in 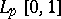 , and the constants
, and the constants 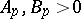 depend only on
depend only on 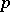 .
.
The Franklin system has had important applications in various questions in analysis. In particular, bases in the spaces 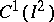 (see [4]) and
(see [4]) and 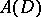 (see [5]) have been constructed using this system. Here
(see [5]) have been constructed using this system. Here 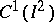 is the space of all continuously-differentiable functions
is the space of all continuously-differentiable functions 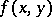 on the square
on the square 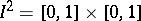 with the norm
with the norm
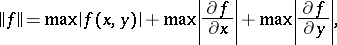 |
and 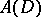 , the disc space, is the space of all functions
, the disc space, is the space of all functions 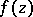 that are analytic in the open disc
that are analytic in the open disc 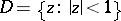 in the complex plane and continuous in the closed disc
in the complex plane and continuous in the closed disc 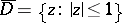 with the norm
with the norm
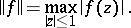 |
The questions of whether there are bases in 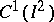 and
and 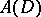 were posed by S. Banach [6].
were posed by S. Banach [6].
References
| [1] | P. Franklin, "A set of continuous orthogonal functions" Math. Ann. , 100 (1928) pp. 522–529 |
| [2] | S. Kaczmarz, H. Steinhaus, "Theorie der Orthogonalreihen" , Chelsea, reprint (1951) |
| [3] | Z. Ciesielski, "Properties of the orthogonal Franklin system" Studia Math. , 23 : 2 (1963) pp. 141–157 |
| [4] | Z. Ciesielski, "A construction of a basis in 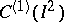 " Studia Math. , 33 : 2 (1969) pp. 243–247 " Studia Math. , 33 : 2 (1969) pp. 243–247 |
| [5] | S.V. Bochkarev, "Existence of a basis in the space of functions analytic in the disk, and some properties of Franklin's system" Math. USSR-Sb. , 24 : 1 (1974) pp. 1–16 Mat. Sb. , 95 : 1 (1974) pp. 3–18 |
| [6] | S.S. Banach, "Théorie des opérations linéaires" , Chelsea, reprint (1955) |
Franklin system. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Franklin_system&oldid=16655