Frölicher-Nijenhuis bracket
Let $M$ be a smooth manifold (cf. also Differentiable manifold) and let $\Omega ^ { k } ( M ; T M ) = \Gamma ( \wedge ^ { k } T ^ { * } M \otimes T M )$. One calls
\begin{equation*} \Omega ( M , T M ) = \oplus _ { k = 0 } ^ { \operatorname { dim } M } \Omega ^ { k } ( M , T M ) \end{equation*}
the space of all vector-valued differential forms. The Frölicher–Nijenhuis bracket $[ \cdot , \cdot ] : \Omega ^ { k } ( M ; T M ) \times \Omega ^ { l } ( M ; T M ) \rightarrow \Omega ^ { k + l } ( M ; T M )$ is a $\bf Z$-graded Lie bracket:
\begin{equation*} [ K , L ] = - ( - 1 ) ^ { k l } [ L , K ], \end{equation*}
\begin{equation*} [ K _ { 1 } , [ K _ { 2 } , K _ { 3 } ] ] = [ [ K _ { 1 } , K _ { 2 } ] , K _ { 3 } ] + ( - 1 ) ^ { k _ { 1 } k _ { 2 } } [ K _ { 2 } , [ K _ { 1 }, K _ { 3 }] ]. \end{equation*}
It extends the Lie bracket of smooth vector fields, since $\Omega ^ { 0 } ( M ; T M ) = \Gamma ( T M ) = \mathcal{X} ( M )$. The identity on $T M$ generates the one-dimensional centre. It is called the Frölicher–Nijenhuis bracket since it appeared with its full properties for the first time in [a1], after some indication in [a8]. One formula for it is:
\begin{equation*} [ \varphi \bigotimes x , \psi \bigotimes Y ] = \end{equation*}
\begin{equation*} = \varphi \bigwedge \psi \bigotimes [ X , Y ] + \varphi \bigwedge {\cal L} _ { X } \psi \bigotimes Y - {\cal L} _ { Y } \varphi \bigwedge \psi \bigotimes X + \end{equation*}
\begin{equation*} + ( - 1 ) ^ { k } \left( d \varphi \bigwedge i _ { X } \psi \bigotimes Y + i _{Y} \varphi \bigwedge d \psi \bigotimes X \right), \end{equation*}
where $X$ and $Y$ are vector fields, $\varphi$ is a $k$-form, and $\psi$ is an $l$-form. It is a bilinear differential operator of bi-degree $( 1,1 )$.
The Frölicher–Nijenhuis bracket is natural in the same way as the Lie bracket for vector fields: if $f : M \rightarrow N$ is smooth and $K _ { i } \in \Omega ^ { k _ { i } } ( M ; T M )$ are $f$-related to $L _ { i } \in \Omega ^ { l } ( N ; T N )$, then $[ K _ { 1 } , K _ { 2 } ]$ is also $f$-related to $L_1$, $L_{2}$.
Details.
A convenient source is [a3], Sect. 8. The basic formulas of the calculus of differential forms extend naturally to include the Frölicher–Nijenhuis bracket: Let
\begin{equation*} \Omega ( M ) = \bigoplus _ { k \geq 0 } \Omega ^ { k } ( M ) = \bigoplus _ { k = 0 } ^ { \operatorname { dim } M } \Gamma \left( \bigwedge^k T ^ { * } M \right) \end{equation*}
be the algebra of differential forms. One denotes by $\operatorname { Der } _ { k } \Omega ( M )$ the space of all (graded) derivations of degree $k$, i.e. all bounded linear mappings $D : \Omega ( M ) \rightarrow \Omega ( M )$ with $D ( \Omega ^ { l } ( M ) ) \subset \Omega ^ { k + l } ( M )$ and $D ( \varphi \wedge \psi ) = D ( \varphi ) \wedge \psi + ( - 1 ) ^ { k l } \varphi \wedge D ( \psi )$ for $\varphi \in \Omega ^ { l } ( M )$. The space $\operatorname { Der }\Omega ( M ) = \oplus _ { k } \operatorname { Der } _ { k } \Omega ( M )$ is a $\bf Z$-graded Lie algebra with the graded commutator $[ D _ { 1 } , D _ { 2 } ] = D _ { 1 } D _ { 2 } - ( - 1 ) ^ { k _ { 1 } k _ { 2 } } D _ { 2 } D _ { 1 }$ as bracket.
A derivation $D \in \operatorname { Der } _ { k } \Omega ( M )$ with $D | _ { \Omega ^ { 0 } } ( M ) = 0$ satisfies $D ( f . \omega ) = f . D ( \omega )$ for $f \in C ^ { \infty } ( M , \mathbf{R} )$, thus $D$ is of tensorial character and induces a derivation $D _ { X } \in \operatorname { Der } _ { k } \wedge T _ { X } ^ { * } M$ for each $x \in M$. It is uniquely determined by its restriction to $1$-forms 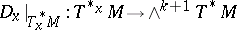 , which can be viewed as an element $K _ { x } \in \wedge ^ { k + 1 } T _ { x } ^ { * } M \otimes T _ { x } M$ depending smoothly on $x \in M$; this is expressed by writing $D = i _ { K }$, where $K \in C ^ { \infty } ( \wedge ^ { k + 1 } T ^ { * } M \otimes T M ) = \Omega ^ { k + 1 } ( M ; T M )$, and one has
, which can be viewed as an element $K _ { x } \in \wedge ^ { k + 1 } T _ { x } ^ { * } M \otimes T _ { x } M$ depending smoothly on $x \in M$; this is expressed by writing $D = i _ { K }$, where $K \in C ^ { \infty } ( \wedge ^ { k + 1 } T ^ { * } M \otimes T M ) = \Omega ^ { k + 1 } ( M ; T M )$, and one has
\begin{equation*} ( i _ { K } \omega ) ( X _ { 1 } , \dots , X _ { k + 1 } ) = \end{equation*}
\begin{equation*} =\frac { 1 } { ( k + 1 ) ! ( l - 1 ) ! } \times \times \sum _ { \sigma \in S _ { k + \text{l} } } \operatorname { sign } \sigma . \omega ( K ( X _ { \sigma 1 } , \ldots , X _ { \sigma ( k + 1 ) } ) , X _ { \sigma ( k + 2 ) } , \ldots ) \end{equation*}
for $\omega \in \Omega ^ { 1 } ( M )$ and $X_i \in \mathcal{X} ( M )$ (or $T _ { x } M$).
By putting $i ( [ K , L ] ^ { \wedge } ) = [ i _ { K } , i _ { L } ]$, one obtains a bracket $[ ., . ] ^ { \wedge }$ on $\Omega ^ { * + 1 } ( M , T M )$ which defines a graded Lie algebra structure with the grading as indicated, and for $K \in \Omega ^ { k + 1 } ( M , T M )$, $L \in \Omega ^ { \text{l} + 1 } ( M , T M )$ one has
\begin{equation*} [ K , L ] \bigwedge = i _ { K } L - ( - 1 ) ^ { k \text{l}} i _ { L } K, \end{equation*}
where $i _ { K } ( \omega \otimes X ) = i _ { K } ( \omega ) \otimes X$. The bracket $[ ., . ] ^ { \wedge }$ is called the Nijenhuis–Richardson bracket, see [a6] and [a7]. If viewed on a vector space $V$, it recognizes Lie algebra structures on $V$: A mapping $P \in L ^ { 2 }_\text { skew } ( V ; V )$ is a Lie bracket if and only if $[ P , P ] ^ { \wedge } = 0$. This can be used to study deformations of Lie algebra structures: $P + A$ is again a Lie bracket on $V$ if and only if $[ P + A , P + A ] ^ { \wedge } = 2 [ P , A ] ^ { \wedge } + [ A , A ] ^ { \wedge } = 0$; this can be written in the form of a Maurer–Cartan equation (cf. also Maurer–Cartan form) as $\delta _ { P } ( A ) + [ A , A ] ^ { \wedge } / 2 = 0$, since $\delta _ { P } = [ P , . ] ^ { \wedge }$ is the coboundary operator for the Chevalley cohomology (cf. also Cohomology) of the Lie algebra $( V , P )$ with values in the adjoint representation $V$. See [a4] for a multi-graded elaboration of this.
The exterior derivative $d$ is an element of $\operatorname { Der } _ { 1 } \Omega ( M )$. In view of the formula $\mathcal{L} _ { X } = [ i_{X} , d ] = i_{X} d + d i _{X}$ for vector fields $X$, one defines for $K \in \Omega ^ { k } ( M ; T M )$ the Lie derivation $\mathcal{L} _ { K } = \mathcal{L} ( K ) \in \operatorname { Der } _ { k } \Omega ( M )$ by $\mathcal{L} _ { K } = [ i _ { K } , d ]$. The mapping ${\cal L} : \Omega ( M , T M ) \rightarrow \operatorname { Der } \Omega ( M )$ is injective. One has $\mathcal{L} ( \operatorname { ld } _ { T M } ) = d$.
For any graded derivation $D \in \operatorname { Der } _ { k } \Omega ( M )$ there are unique $K \in \Omega ^ { k } ( M ; T M )$ and $L \in \Omega ^ { k + 1 } ( M ; T M )$ such that
\begin{equation*} D = \mathcal{L} _ { K } + i _ { L }. \end{equation*}
One has $L = 0$ if and only if $[ D , d ] = 0$. Moreover, $D | _ { \Omega ^ { 0 } ( M ) } = 0$ if and only if $K = 0$.
Let $K \in \Omega ^ { k } ( M ; T M )$ and $L \in \Omega ^ { 1 } ( M ; T M )$. Then, obviously, $[ [ \mathcal{L} _ { K } , \mathcal{L} _ { L } ] , d ] = 0$, so
\begin{equation*} [ \mathcal{L} ( K ) , \mathcal{L} ( L ) ] = \mathcal{L} ( [ K , L ] ) \end{equation*}
for a uniquely defined $[ K , L ] \in \Omega ^ { k + 1 } ( M ; T M )$. This vector-valued form $[ K , L ]$ is the Frölicher–Nijenhuis bracket of $K$ and $L$.
For $K \in \Omega ^ { k } ( M ; T M )$ and $L \in \Omega ^ { \text{l} + 1 } ( M ; T M )$ one has
\begin{equation*} [\mathcal{L} _ { K } , i _ { L } ] = i ( [ K , L ] ) - ( - 1 ) ^ { k \text{l} } \mathcal{L} ( i _ { L } K ). \end{equation*}
The space $\operatorname{Der} \Omega ( M )$ is a graded module over the graded algebra $\Omega ( M )$ with the action $( \omega \wedge D ) \varphi = \omega \wedge D ( \varphi )$, because $\Omega ( M )$ is graded commutative. Let the degree of $\omega$ be $q$, of $\varphi$ be $k$, and of $\psi$ be $\operatorname{l}$. Let the other degrees be as indicated. Then:
\begin{equation*} [ \omega \wedge D _ { 1 } , D _ { 2 } ] = \end{equation*}
\begin{equation*} = \omega \bigwedge [ D _ { 1 } , D _ { 2 } ] - ( - 1 ) ^ { ( q + k _ { 1 } ) k _ { 2 } } D _ { 2 } ( \omega ) \bigwedge D _ { 1 } ,\, i ( \omega \bigwedge L ) = \omega \bigwedge i ( L ), \end{equation*}
\begin{equation*} \omega \bigwedge \mathcal{L} _ { K } = \mathcal{L} ( \omega \bigwedge K ) + ( - 1 ) ^ { q + k - 1 } i ( d \omega \bigwedge K ) ,\, [ \omega \bigwedge L _ { 1 } , L _ { 2 } ] ^ { \bigwedge } = \omega \bigwedge [ L _ { 1 } , L _ { 2 } ] + \end{equation*}
\begin{equation*} - ( - 1 ) ^ { ( q + \operatorname{l} _ { 1 } - 1 ) ( \operatorname{l} _ { 2 } - 1 ) } i ( L _ { 2 } ) \omega \bigwedge L _ { 1 } , [ \omega \bigwedge K _ { 1 } , K _ { 2 } ] = \omega \bigwedge [ K _ { 1 } , K _ { 2 } ] + \end{equation*}
\begin{equation*} - ( - 1 ) ^ { ( q + k _ { 1 } ) k _ { 2 } } \mathcal{L} ( K _ { 2 } ) \omega \bigwedge K _ { 1 } + \end{equation*}
\begin{equation*} + ( - 1 ) ^ { q + k _ { 1 } } d \omega \bigwedge i ( K _ { 1 } ) K _ { 2 }. \end{equation*}
For $K \in \Omega ^ { k } ( M ; T M )$ and $\omega \in \Omega ^ { 1 } ( M )$, the Lie derivative of $\omega$ along $K$ is given by:
\begin{equation*} ( \mathcal{L} _ { K } \omega ) ( X _ { 1 } , \dots , X _ { k + 1 } ) = \end{equation*}
\begin{equation*} = \frac { 1 } { k ! \text{l} ! } \sum _ { \sigma } \operatorname { sign } \sigma \times \times \mathcal{L} ( K(X _ { \sigma 1 } , \ldots , X _ { \sigma k } ) ) ( \omega ( X _ { \sigma ( k + 1 ) } , \ldots , X _ { \sigma ( k + 1 ) } ) ) + \end{equation*}
\begin{equation*} +\frac { - 1 } { k ! ( \text{l} - 1 ) ! } \times \times \sum _ { \sigma } \operatorname { sign } \sigma \omega ( [ K ( X _ { \sigma 1 } , \ldots , X _ { \sigma k } ) , X _ { \sigma ( k + 1 ) } ] , X _ { \sigma ( k + 2 ) } , \ldots )+ \end{equation*}
\begin{equation*} + \frac { ( - 1 ) ^ { k - 1 } } { ( k - 1 ) ! ( 1 - 1 ) ! 2 ! } \times \times \sum _ { \sigma } \operatorname { sign } \ \sigma \ \omega ( K ( [ X _ { \sigma 1 } , X _ { \sigma 2 } ] , X _ { \sigma 3 } , \ldots ) , X _ { \sigma ( k + 2 ) } , \ldots ). \end{equation*}
For $K \in \Omega ^ { k } ( M ; T M )$ and $L \in \Omega ^ { 1 } ( M ; T M )$, the Frölicher–Nijenhuis bracket $[ K , L ]$ is given by:
\begin{equation*} [ K , L ] ( X _ { 1 } , \dots , X _ { k + 1 } ) = \end{equation*}
\begin{equation*} = \frac { 1 } { k ! l ! } \sum _ { \sigma } \operatorname { sign } \sigma \times \times [ K ( X _ { \sigma 1 } , \ldots , X _ { \sigma k } ) , L ( X _ { \sigma ( k + 1 ) } , \ldots , X _ { \sigma ( k + 1 ) } ) ] + \end{equation*}
\begin{equation*} + \frac { - 1 } { k ! ( \operatorname {l} - 1 ) ! } \sum _ { \sigma } \operatorname { sign } \sigma \times \times L ( [ K ( X _ { \sigma 1 } , \ldots , X _ { \sigma k } ) , X _ { \sigma ( k + 1 ) } ] , X _ { \sigma ( k + 2 ) } , \ldots )+ \end{equation*}
\begin{equation*} + \frac { ( - 1 ) ^ { k \text{l} } } { ( k - 1 ) ! \text{l}! } \sum _ { \sigma } \operatorname { sign } \sigma \times \times K ( [ L ( X _ { \sigma 1 } , \ldots , X _ { \sigma \text{l} } ) , X _ { \sigma ( \text{l} + 1 ) } ] , X _ { \sigma ( \text{l} + 2 ) } , \ldots ) + \end{equation*}
\begin{equation*} + \frac { ( - 1 ) ^ { k - 1 } } { ( k - 1 ) ! ( 1 - 1 ) ! 2 ! } \times \times \sum _ { \sigma } \operatorname { sign } \sigma L ( K ( [ X _ { \sigma 1 } , X _ { \sigma 2 } ] , X _ { \sigma 3 } , \ldots ) , X _ { \sigma ( k + 2 ) } , \ldots ) + \end{equation*}
\begin{equation*} +\frac { ( - 1 ) ^ { ( k - 1 ) \text{l} } } { ( k - 1 ) ! ( \text{l} - 1 ) ! 2 ! } \times \times \sum _ { \sigma } \operatorname { sign } \sigma\, K ( L ( [ X _ { \sigma 1 } , X _ { \sigma 2 } ] , X _ { \sigma 3 } , \ldots ) , X _ { \sigma ( \text{l} + 2 ) , \ldots } ). \end{equation*}
The Frölicher–Nijenhuis bracket expresses obstructions to integrability in many different situations: If $J : T M \rightarrow T M$ is an almost-complex structure, then $J$ is complex structure if and only if the Nijenhuis tensor $[ J , J ]$ vanishes (the Newlander–Nirenberg theorem, [a5]). If $P : T M \rightarrow T M$ is a fibre-wise projection on the tangent spaces of a fibre bundle $M \rightarrow B$, then $[ P , P ]$ is a version of the curvature (see [a3], Sects. 9; 10). If $A : T M \rightarrow T M$ is fibre-wise diagonalizable with all eigenvalues real and of constant multiplicity, then the eigenspaces of $A$ are integrable if and only if $[ A , A ] = 0$.
References
| [a1] | A. Frölicher, A. Nijenhuis, "Theory of vector valued differential forms. Part I." Indag. Math. , 18 (1956) pp. 338–359 |
| [a2] | A. Frölicher, A. Nijenhuis, "Invariance of vector form operations under mappings" Comment. Math. Helvetici , 34 (1960) pp. 227–248 |
| [a3] | I. Kolář, Peter W. Michor, J. Slovák, "Natural operations in differential geometry" , Springer (1993) |
| [a4] | Pierre Lecomte, Peter W. Michor, Hubert Schicketanz, "The multigraded Nijenhuis–Richardson Algebra, its universal property and application" J. Pure Appl. Algebra , 77 (1992) pp. 87–102 |
| [a5] | A. Newlander, L. Nirenberg, "Complex analytic coordinates in almost complex manifolds" Ann. of Math. , 65 (1957) pp. 391–404 |
| [a6] | A. Nijenhuis, R. Richardson, "Cohomology and deformations in graded Lie algebras" Bull. Amer. Math. Soc. , 72 (1966) pp. 1–29 |
| [a7] | A. Nijenhuis, R. Richardson, "Deformation of Lie algebra structures" J. Math. Mech. , 17 (1967) pp. 89–105 |
| [a8] | J.A. Schouten, "Über Differentialkonkomitanten zweier kontravarianten Grössen" Indag. Math. , 2 (1940) pp. 449–452 |
Frölicher-Nijenhuis bracket. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fr%C3%B6licher-Nijenhuis_bracket&oldid=50955