Fock space
Fok space
In the simplest and most often used case, a Hilbert space consisting of infinite sequences of the form
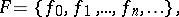 | (1) |
where
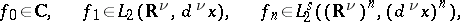 |
or
 |
in which
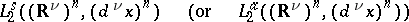 |
denotes the Hilbert space of symmetric (respectively, anti-symmetric) functions in  variables
variables 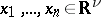 ,
, 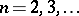 . The scalar product of two sequences
. The scalar product of two sequences 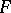 and
and 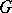 of the form (1) is equal to
of the form (1) is equal to
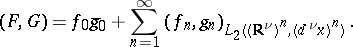 |
In the case when the sequences 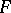 consist of symmetric functions, one speaks of a symmetric (or boson) Fock space, and in the case of sequences of anti-symmetric functions the Fock space is called anti-symmetric (or fermion). Fock spaces were first introduced by V.A. Fock [V.A. Fok] [1] in this simplest case.
consist of symmetric functions, one speaks of a symmetric (or boson) Fock space, and in the case of sequences of anti-symmetric functions the Fock space is called anti-symmetric (or fermion). Fock spaces were first introduced by V.A. Fock [V.A. Fok] [1] in this simplest case.
In the general case of an arbitrary Hilbert space 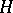 , the Fock space
, the Fock space 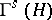 (or
(or 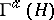 ) constructed over
) constructed over 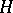 is the symmetrized (or anti-symmetrized) tensor exponential of
is the symmetrized (or anti-symmetrized) tensor exponential of 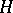 , that is, the space
, that is, the space
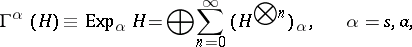 | (2) |
where the symbol  denotes the direct orthogonal sum of Hilbert spaces,
denotes the direct orthogonal sum of Hilbert spaces, 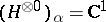 ,
,  , and
, and 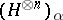 ,
, 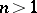 , is for
, is for 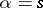 the symmetrized or for
the symmetrized or for  the anti-symmetrized
the anti-symmetrized  -th tensor power of
-th tensor power of 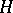 . In the case
. In the case 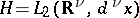 definition (2) is equivalent to the definition of a Fock space given at the beginning of the article, if one identifies the spaces
definition (2) is equivalent to the definition of a Fock space given at the beginning of the article, if one identifies the spaces 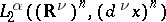 and
and 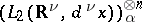 so that the tensor product
so that the tensor product
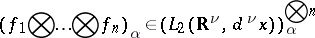 |
of the sequence of functions
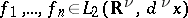 |
corresponds to the function
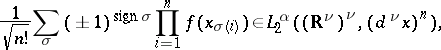 | (3) |
where the summation is taken over all permutations 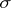 of the indices
of the indices 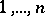 ;
; 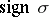 is the sign of
is the sign of 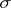 , and the sign
, and the sign 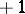 or
or 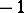 in (3) corresponds to the symmetric or anti-symmetric case.
in (3) corresponds to the symmetric or anti-symmetric case.
In quantum mechanics, the Fock spaces 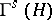 or
or 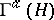 serve as the state spaces of quantum-mechanical systems consisting of an arbitrary (but finite) number of identical particles such that the state space of each separate particle is
serve as the state spaces of quantum-mechanical systems consisting of an arbitrary (but finite) number of identical particles such that the state space of each separate particle is 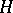 . Here, depending on which of the Fock spaces — the symmetric
. Here, depending on which of the Fock spaces — the symmetric  or the anti-symmetric
or the anti-symmetric 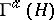 — describes this system, the particles themselves are called bosons or fermions, respectively. For every
— describes this system, the particles themselves are called bosons or fermions, respectively. For every 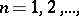 the subspace
the subspace 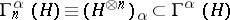 ,
, 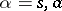 , is called the
, is called the  -particle subspace: The vectors in it describe those states in which there are exactly
-particle subspace: The vectors in it describe those states in which there are exactly  particles; the unit vector
particles; the unit vector 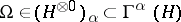 ,
, 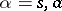 (in the notation of (1):
(in the notation of (1): 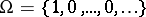 ), called the vacuum vector, describes the state of the system in which there are no particles.
), called the vacuum vector, describes the state of the system in which there are no particles.
In studying linear operators acting on the Fock spaces 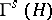 and
and 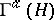 , one often applies a special formalism called the method of second quantization. It is based on introducing two families of linear operators on each of the spaces
, one often applies a special formalism called the method of second quantization. It is based on introducing two families of linear operators on each of the spaces 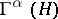 : the so-called annihilation operators
: the so-called annihilation operators 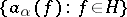 ,
, 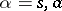 , and the family of operators adjoint to them
, and the family of operators adjoint to them 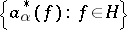 , called creation operators. The annihilation operators are given as the closures of the operators acting on the vectors
, called creation operators. The annihilation operators are given as the closures of the operators acting on the vectors
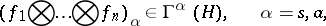 | (4) |
where 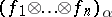 are the symmetrized (for
are the symmetrized (for 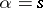 ) or anti-symmetrized
) or anti-symmetrized 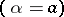 tensor products of the sequences of vectors
tensor products of the sequences of vectors 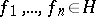 ,
, 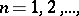 according to the formulas
according to the formulas
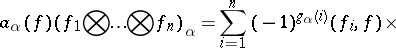 |
 |
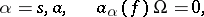 |
where 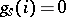 and
and 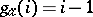 . The creation operators
. The creation operators 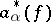 act on the vectors (3) according to the formulas
act on the vectors (3) according to the formulas
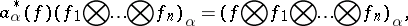 |
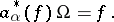 |
Here for every 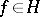 ,
, 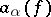 :
: 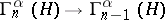 ,
, 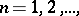 and
and 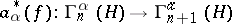 ,
,  that is, states of the physical system with
that is, states of the physical system with  particles are mapped by the annihilation operators
particles are mapped by the annihilation operators 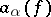 to states with
to states with 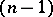 particles, and by the creation operators
particles, and by the creation operators 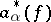 to states with
to states with 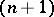 particles. Creation and annihilation operators occur in many cases of a similar system as "generators" in the collection of all operators (bounded and unbounded) acting on Fock spaces. The representation of such operators in the form of a sum (finite or infinite) of operators of the form
particles. Creation and annihilation operators occur in many cases of a similar system as "generators" in the collection of all operators (bounded and unbounded) acting on Fock spaces. The representation of such operators in the form of a sum (finite or infinite) of operators of the form
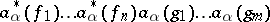 |
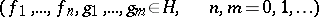 |
— the so-called normal form of an operator — and methods of dealing with operators based on such a representation (computing functions of them, reducing operators to the "simplest" form, various examples of approximation, etc.) also constitute the content of the formalism of second quantization mentioned above (see [2]).
In the case of a symmetric Fock space over a real space 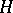 there is a canonical isomorphism between that space and the Hilbert space of square-integrable functionals in a Gaussian linear random process
there is a canonical isomorphism between that space and the Hilbert space of square-integrable functionals in a Gaussian linear random process 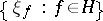 defined on
defined on 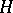 such that
such that
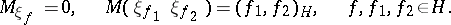 |
This isomorphism, called the Itô–Segal–Wick mapping, is uniquely determined by the condition that for any orthonormal system of elements 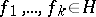 and any collection of non-negative integers
and any collection of non-negative integers  the vector
the vector
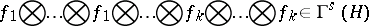 |
(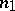 times
times 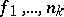 times
times 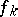 ) is mapped to the functional
) is mapped to the functional
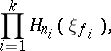 |
where the 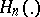 ,
, 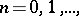 are the Hermite polynomials with leading coefficient one (see [3], [4]).
are the Hermite polynomials with leading coefficient one (see [3], [4]).
References
| [1] | V. Fock, Z. Phys. , 75 (1932) pp. 622–647 |
| [2] | F.A. Berezin, "The method of second quantization" , Acad. Press (1966) (Translated from Russian) (Revised (augmented) second edition: Kluwer, 1989) |
| [3] | R.L. Dobrushin, R.A. Minlos, "Polynomials in linear random functions" Russian Math. Surveys , 32 : 2 (1971) pp. 71–127 Uspekhi Mat. Nauk , 32 : 2 (1977) pp. 67–122 |
| [4] | B. Simon, "The 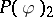 Euclidean (quantum) field theory" , Princeton Univ. Press (1974) Euclidean (quantum) field theory" , Princeton Univ. Press (1974) |
Comments
The number operator 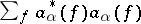 ,
, 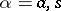 , where
, where 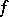 runs through an orthonormal basis of
runs through an orthonormal basis of 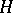 , has as eigen spaces with eigen value
, has as eigen spaces with eigen value  the spaces
the spaces 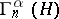 . It is interpreted as giving the number of particles.
. It is interpreted as giving the number of particles.
Fock spaces also play an important role in stochastic integration (including fermionic integration), cf. Stochastic integral, and in white noise analysis.
References
| [a1] | N.N. [N.N. Bogolyubov] Bogolubov, A.A. Logunov, I.T. Todorov, "Introduction to axiomatic quantum field theory" , Benjamin (1975) (Translated from Russian) |
| [a2] | P.J.M. Bongaarts, "The mathematical structure of free quantum fields. Gaussian systems" E.A. de Kerf (ed.) H.G.J. Pijls (ed.) , Proc. Seminar. Mathematical structures in field theory , CWI, Amsterdam (1984–1986) pp. 1–50 |
Fock space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fock_space&oldid=13259