Floquet theory
A theory concerning the structure of the space of solutions, and the properties of solutions, of a linear system of differential equations with periodic coefficients
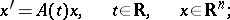 | (1) |
the matrix  is periodic in
is periodic in  with period
with period  and is summable on every compact interval in
and is summable on every compact interval in  .
.
1) Every fundamental matrix  of the system (1) has a representation
of the system (1) has a representation
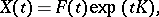 | (2) |
called the Floquet representation (see [1]), where  is some
is some  -periodic matrix and
-periodic matrix and  is some constant matrix. There is a basis
is some constant matrix. There is a basis  of the space of solutions of (1) such that
of the space of solutions of (1) such that  has Jordan form in this basis; this basis can be represented in the form
has Jordan form in this basis; this basis can be represented in the form
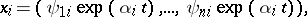 |
where 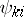 are polynomials in
are polynomials in 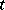 with
with 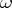 -periodic coefficients, and the
-periodic coefficients, and the 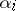 are the characteristic exponents (cf. Characteristic exponent) of the system (1). Every component of a solution of (1) is a linear combination of functions of the form (of the Floquet solutions)
are the characteristic exponents (cf. Characteristic exponent) of the system (1). Every component of a solution of (1) is a linear combination of functions of the form (of the Floquet solutions) 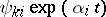 . In the case when all the characteristic exponents are distinct (or if there are multiple ones among them, but they correspond to simple elementary divisors), the
. In the case when all the characteristic exponents are distinct (or if there are multiple ones among them, but they correspond to simple elementary divisors), the 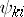 are simply
are simply  -periodic functions. The matrices
-periodic functions. The matrices 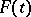 and
and  in the representation (2) are, generally speaking, complex valued. If one restricts oneself just to the real case, then
in the representation (2) are, generally speaking, complex valued. If one restricts oneself just to the real case, then 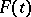 does not have to be
does not have to be  -periodic, but must be
-periodic, but must be 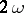 -periodic.
-periodic.
2) The system (1) can be reduced to a differential equation with a constant matrix,  , by means of the Lyapunov transformation
, by means of the Lyapunov transformation
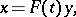 | (3) |
where  and
and  are the matrices from the Floquet representation (2) (see [2]). The combination of representation (2) together with the substitution (3) is often called the Floquet–Lyapunov theorem.
are the matrices from the Floquet representation (2) (see [2]). The combination of representation (2) together with the substitution (3) is often called the Floquet–Lyapunov theorem.
3) Let  be the spectrum of the matrix
be the spectrum of the matrix  . For every
. For every  such that
such that  ,
, 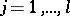 , in view of (2) the space
, in view of (2) the space 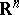 splits into the direct sum of two subspaces
splits into the direct sum of two subspaces 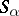 and
and 
 |
such that
 |
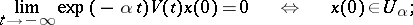 |
here  is the fundamental matrix of (1) normalized at zero. This implies exponential dichotomy of (1) if
is the fundamental matrix of (1) normalized at zero. This implies exponential dichotomy of (1) if  for any
for any 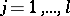 .
.
References
| [1] | G. Floquet, Ann. Sci. Ecole Norm. Sup. , 12 : 2 (1883) pp. 47–88 |
| [2] | A.M. Lyapunov, "Problème général de la stabilité du mouvement" , Collected works , 2 , Princeton Univ. Press , Moscow-Leningrad (1956) pp. 7–263 (In Russian) |
| [3] | B.P. Demidovich, "Lectures on the mathematical theory of stability" , Moscow (1967) (In Russian) |
| [4] | V.A. Yakubovich, V.M. Starzhinskii, "Linear differential equations with periodic coefficients" , Wiley (1975) (Translated from Russian) |
| [5] | J.L. Massera, J.J. Shäffer, "Linear differential equations and function spaces" , Acad. Press (1966) |
| [6] | N.P. Erugin, "Linear systems of ordinary differential equations with periodic and quasi-periodic coefficients" , Acad. Press (1966) (Translated from Russian) |
Comments
References
| [a1] | J.K. Hale, "Ordinary differential equations" , Wiley (1969) |
| [a2] | P. Hartman, "Ordinary differential equations" , Birkhäuser (1982) |
Floquet theory. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Floquet_theory&oldid=18199