Exact endomorphism

of a Lebesgue space

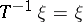
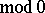An endomorphism of (cf. Metric isomorphism) such that the only measurable decomposition that is coarser than all , where is the decomposition into points, is the trivial decomposition with as only element all of . An equivalent definition is: There is no measurable decomposition that is invariant (in older terminology — totally invariant) under (i.e. is such that ). Examples of such endomorphisms are a one-sided Bernoulli shift and an expanding mapping.

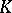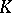Exact endomorphisms have strong ergodic properties analogous to those of -systems (to which they are related: there is a construction associating an automorphism to some endomorphism — its natural extension; for an exact endomorphism the latter is a -automorphism). Cf. -system.

References

[1]	V.A. Rokhlin, "Exact endomorphisms of a Lebesgue space" Izv. Akad. Nauk SSSR Ser. Mat. , 25 : 4 (1961) pp. 499–530 (In Russian)
[2]	I.P. [I.P. Kornfel'd] Cornfel'd, S.V. Fomin, Ya.G. Sinai, "Ergodic theory" , Springer (1982) (Translated from Russian)

Comments

Instead of "(measurable) decomposition" one also uses (measurable) partition.

The usual definition is as follows: An endomorphism 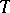of a Lebesgue space 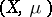is said to be exact whenever 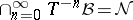, where 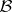is the given 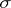-algebra of 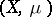and 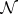is the 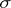-algebra of subsets of measure 0 or 1. For a proof that expanding mappings are exact with respect to some measure, see e.g. [a1], Sect. III.1.

References

[a1]	R. Mañé, "Ergodic theory and differentiable dynamics" , Springer (1987)