One of the possible measures for characterizing the accuracy of information reproduction over a communication channel (see also Information, exactness of reproducibility of). For the transmission of information 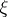 from a source which has
from a source which has 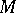 different possible values
different possible values 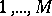 with probability distribution
with probability distribution 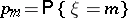 ,
,  , a certain communication channel is used. Then for fixed methods of coding and decoding (see also Information, transmission of), the probability of erroneous decoding
, a certain communication channel is used. Then for fixed methods of coding and decoding (see also Information, transmission of), the probability of erroneous decoding 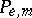 ,
,  , is defined by
, is defined by
where 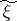 is the decoded message at the channel output. The variable quantity
is the decoded message at the channel output. The variable quantity
is called the mean probability of erroneous decoding. The study of the optimal probability of erroneous decoding, 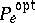 , defined by
, defined by
is of particular interest. The infimum is taken over all possible methods of coding and decoding. Owing to the difficulty of obtaining an accurate expression for 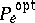 , which is caused by the fact that optimal coding methods are usually unknown, the study of the asymptotic behaviour of
, which is caused by the fact that optimal coding methods are usually unknown, the study of the asymptotic behaviour of 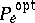 when the length of the message in the channel increases is of interest. More precisely, the following situation is studied. Let a segment of length
when the length of the message in the channel increases is of interest. More precisely, the following situation is studied. Let a segment of length 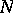 in a communication channel with discrete time be used, and put
in a communication channel with discrete time be used, and put 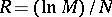 . The asymptotic behaviour of
. The asymptotic behaviour of 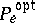 has to be studied when
has to be studied when 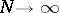 and
and 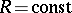 (this means that the length of the message increases, while its transmission rate remains constant). If the channel is a homogeneous memoryless channel with discrete time and if the spaces
(this means that the length of the message increases, while its transmission rate remains constant). If the channel is a homogeneous memoryless channel with discrete time and if the spaces 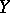 and
and 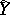 of values of the components of the input and output signals are finite, then the following upper and lower bounds for
of values of the components of the input and output signals are finite, then the following upper and lower bounds for 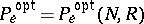 are known:
are known:
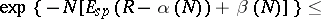 | (1) |
where 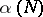 and
and 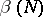 tend to zero with increasing
tend to zero with increasing 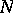 , while the functions
, while the functions 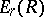 and
and 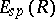 are defined as follows:
are defined as follows:
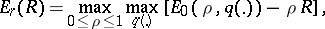 | (2) |
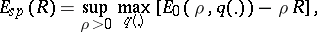 | (3) |
where
Here, 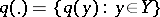 is an arbitrary probability distribution on
is an arbitrary probability distribution on 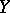 ,
, 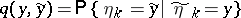 ,
, 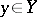 ,
, 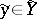 , while
, while 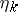 and
and 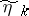 ,
, 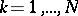 , are the components of the input and output signals of the memoryless channel being considered. It is known that
, are the components of the input and output signals of the memoryless channel being considered. It is known that 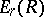 and
and 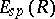 , defined by the formulas (2) and (3), are positive, convex from below, monotone decreasing functions of
, defined by the formulas (2) and (3), are positive, convex from below, monotone decreasing functions of 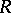 when
when 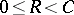 , where
, where 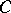 is the transmission rate of the channel (cf. Transmission rate of a channel), and that
is the transmission rate of the channel (cf. Transmission rate of a channel), and that 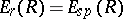 when
when 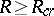 ; here
; here 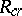 is a quantity defined by the transition matrix of the channel and called the critical speed of the given memoryless channel. Thus, for values
is a quantity defined by the transition matrix of the channel and called the critical speed of the given memoryless channel. Thus, for values 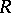 ,
, 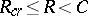 , the main terms of the upper and lower bounds (1) for
, the main terms of the upper and lower bounds (1) for 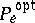 coincide asymptotically, hence for this range of
coincide asymptotically, hence for this range of 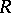 the exact value of the reliability function of the channel,
the exact value of the reliability function of the channel, 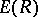 , defined by
, defined by
is known. For values of 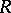 ,
, 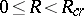 , the exact value of
, the exact value of 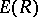 for arbitrary memoryless channels is still unknown (1983), although the bounds (1) can still be improved. The exponential character of decrease of
for arbitrary memoryless channels is still unknown (1983), although the bounds (1) can still be improved. The exponential character of decrease of 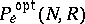 has been proved for a very broad class of channels.
has been proved for a very broad class of channels.
References
| [1] | R. Gallager, "Information theory and reliable communication" , 1–2 , Wiley (1968–1972) |
| [2] | A.A. Feinstein, "Foundations of information theory" , McGraw-Hill (1958) |
How to Cite This Entry:
Erroneous decoding, probability of. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Erroneous_decoding,_probability_of&oldid=14369
This article was adapted from an original article by R.L. DobrushinV.V. Prelov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098.
See original article from a source which has
from a source which has 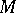 different possible values
different possible values 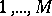 with probability distribution
with probability distribution 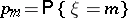 ,
,  , a certain communication channel is used. Then for fixed methods of coding and decoding (see also Information, transmission of), the probability of erroneous decoding
, a certain communication channel is used. Then for fixed methods of coding and decoding (see also Information, transmission of), the probability of erroneous decoding 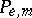 ,
,  , is defined by
, is defined by
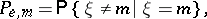
 is the decoded message at the channel output. The variable quantity
is the decoded message at the channel output. The variable quantity
 , defined by
, defined by
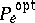 , which is caused by the fact that optimal coding methods are usually unknown, the study of the asymptotic behaviour of
, which is caused by the fact that optimal coding methods are usually unknown, the study of the asymptotic behaviour of 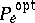 when the length of the message in the channel increases is of interest. More precisely, the following situation is studied. Let a segment of length
when the length of the message in the channel increases is of interest. More precisely, the following situation is studied. Let a segment of length 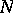 in a communication channel with discrete time be used, and put
in a communication channel with discrete time be used, and put 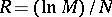 . The asymptotic behaviour of
. The asymptotic behaviour of 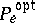 has to be studied when
has to be studied when 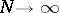 and
and 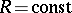 (this means that the length of the message increases, while its transmission rate remains constant). If the channel is a homogeneous memoryless channel with discrete time and if the spaces
(this means that the length of the message increases, while its transmission rate remains constant). If the channel is a homogeneous memoryless channel with discrete time and if the spaces 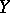 and
and 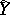 of values of the components of the input and output signals are finite, then the following upper and lower bounds for
of values of the components of the input and output signals are finite, then the following upper and lower bounds for 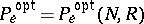 are known:
are known:
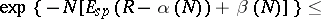
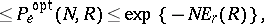
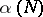 and
and 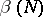 tend to zero with increasing
tend to zero with increasing 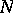 , while the functions
, while the functions 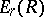 and
and 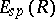 are defined as follows:
are defined as follows:
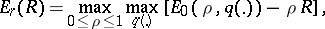
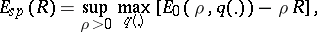
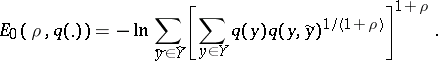
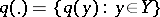 is an arbitrary probability distribution on
is an arbitrary probability distribution on 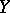 ,
, 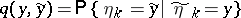 ,
, 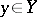 ,
, 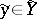 , while
, while 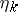 and
and 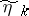 ,
, 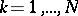 , are the components of the input and output signals of the memoryless channel being considered. It is known that
, are the components of the input and output signals of the memoryless channel being considered. It is known that 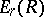 and
and 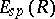 , defined by the formulas (2) and (3), are positive, convex from below, monotone decreasing functions of
, defined by the formulas (2) and (3), are positive, convex from below, monotone decreasing functions of 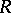 when
when 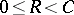 , where
, where 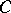 is the transmission rate of the channel (cf. Transmission rate of a channel), and that
is the transmission rate of the channel (cf. Transmission rate of a channel), and that 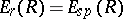 when
when 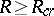 ; here
; here 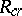 is a quantity defined by the transition matrix of the channel and called the critical speed of the given memoryless channel. Thus, for values
is a quantity defined by the transition matrix of the channel and called the critical speed of the given memoryless channel. Thus, for values 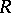 ,
, 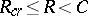 , the main terms of the upper and lower bounds (1) for
, the main terms of the upper and lower bounds (1) for 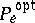 coincide asymptotically, hence for this range of
coincide asymptotically, hence for this range of 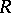 the exact value of the reliability function of the channel,
the exact value of the reliability function of the channel, 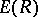 , defined by
, defined by
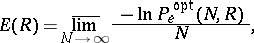
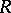 ,
, 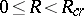 , the exact value of
, the exact value of 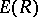 for arbitrary memoryless channels is still unknown (1983), although the bounds (1) can still be improved. The exponential character of decrease of
for arbitrary memoryless channels is still unknown (1983), although the bounds (1) can still be improved. The exponential character of decrease of 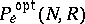 has been proved for a very broad class of channels.
has been proved for a very broad class of channels.