Elliptic curve
A non-singular complete algebraic curve of genus 1. The theory of elliptic curves is the source of a large part of contemporary algebraic geometry. But historically the theory of elliptic curves arose as a part of analysis, as the theory of elliptic integrals and elliptic functions (cf. Elliptic integral; Elliptic function).
Examples. A non-singular plane projective cubic curve; the intersection of two non-singular quadrics in three-dimensional projective space; a two-sheeted covering of the projective line ramified at exactly four points; and also a one-dimensional Abelian variety are elliptic curves.
The geometry of an elliptic curve.
Let 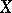 be an elliptic curve over an algebraically closed field
be an elliptic curve over an algebraically closed field  . Then
. Then 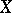 is biregularly isomorphic to a plane cubic curve (see [1], [9], [13]). If
is biregularly isomorphic to a plane cubic curve (see [1], [9], [13]). If 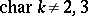 , then in the projective plane
, then in the projective plane 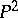 there is an affine coordinate system in which the equation of
there is an affine coordinate system in which the equation of 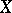 is in normal Weierstrass form:
is in normal Weierstrass form:
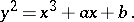 | (1) |
The curve 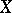 is non-singular if and only if the polynomial
is non-singular if and only if the polynomial  does not have multiple zeros, that is, if the discriminant
does not have multiple zeros, that is, if the discriminant 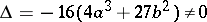 . In
. In 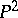 the curve (1) has a unique point at infinity, which is denoted by
the curve (1) has a unique point at infinity, which is denoted by 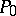 ;
; 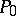 is a point of inflection of (1), and the tangent at
is a point of inflection of (1), and the tangent at 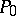 is the line at infinity. The
is the line at infinity. The  -invariant of an elliptic curve
-invariant of an elliptic curve 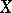 ,
,
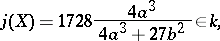 |
does not depend on the choice of the coordinate system. Two elliptic curves have the same 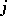 -invariant if and only if they are biregularly isomorphic. For any
-invariant if and only if they are biregularly isomorphic. For any 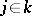 there is an elliptic curve
there is an elliptic curve  over
over 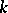 with
with  .
.
The group structure on an elliptic curve.
Let  be a fixed point on an elliptic curve
be a fixed point on an elliptic curve  . The mapping
. The mapping 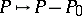 assigning to a point
assigning to a point  the divisor
the divisor 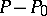 on
on 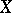 establishes a one-to-one correspondence between
establishes a one-to-one correspondence between 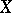 and the group
and the group 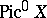 of divisor classes of degree
of divisor classes of degree  on
on  , that is, the Picard variety of
, that is, the Picard variety of 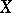 . This correspondence endows
. This correspondence endows 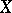 with the structure of an Abelian group that is compatible with the structure of an algebraic variety and that turns
with the structure of an Abelian group that is compatible with the structure of an algebraic variety and that turns 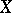 into a one-dimensional Abelian variety
into a one-dimensional Abelian variety  ; here
; here  is the trivial element of the group. This group structure has the following geometric description. Let
is the trivial element of the group. This group structure has the following geometric description. Let  be a smooth plane cubic curve. Then the sum of two points
be a smooth plane cubic curve. Then the sum of two points 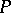 and
and 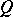 is defined by the rule
is defined by the rule  , where
, where 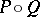 is the third point of intersection of
is the third point of intersection of 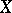 with the line passing through
with the line passing through 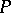 and
and 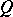 . In other words, the sum of three points on
. In other words, the sum of three points on 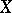 vanishes if and only if the points are collinear.
vanishes if and only if the points are collinear.
An elliptic curve as a one-dimensional Abelian variety.
Let 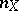 denote the endomorphism of multiplication by
denote the endomorphism of multiplication by  in
in 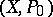 . If
. If 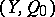 is an elliptic curve with distinguished point
is an elliptic curve with distinguished point 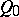 , then any rational mapping
, then any rational mapping 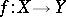 has the form
has the form 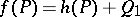 , where
, where  and
and 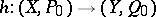 is a homomorphism of Abelian varieties. Here
is a homomorphism of Abelian varieties. Here  is either a constant mapping at
is either a constant mapping at 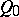 or is an isogeny, that is, there is a homomorphism of Abelian varieties
or is an isogeny, that is, there is a homomorphism of Abelian varieties  such that
such that 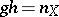 and
and 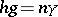 for some
for some  (see [1], [6]).
(see [1], [6]).
The automorphism group of an elliptic curve 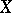 acts transitively on
acts transitively on 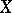 , and its subgroup
, and its subgroup  of automorphisms leaving
of automorphisms leaving  fixed is non-trivial and finite. Suppose that
fixed is non-trivial and finite. Suppose that 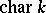 is not
is not  or
or  . When
. When 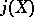 is neither 0 nor
is neither 0 nor 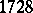 , then
, then  consists of the two elements
consists of the two elements 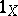 and
and  . The order of
. The order of 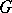 is 4 when
is 4 when 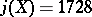 and 6 when
and 6 when 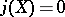 (see [1], [6], [13]).
(see [1], [6], [13]).
An important invariant of an elliptic curve is the endomorphism ring 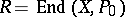 of the Abelian variety
of the Abelian variety 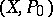 . The mapping
. The mapping  defines an imbedding of
defines an imbedding of 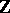 in
in  . If
. If 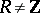 , one says that
, one says that  is an elliptic curve with complex multiplication. The ring
is an elliptic curve with complex multiplication. The ring 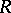 can be of one of the following types (see [1], [9], [13]): I)
can be of one of the following types (see [1], [9], [13]): I) 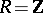 ; II)
; II) 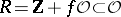 , where
, where  is the ring of algebraic integers of an imaginary quadratic field
is the ring of algebraic integers of an imaginary quadratic field  and
and 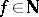 ; or III)
; or III) 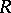 is a non-commutative
is a non-commutative 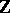 -algebra of rank 4 without divisors of zero. In this case
-algebra of rank 4 without divisors of zero. In this case 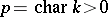 and
and 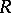 is a maximal order in the quaternion algebra over
is a maximal order in the quaternion algebra over  ramified only at
ramified only at  and
and 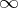 . Such elliptic curves exist for all
. Such elliptic curves exist for all 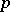 and are called supersingular; elliptic curves in characteristic
and are called supersingular; elliptic curves in characteristic  that are not supersingular are said to be ordinary.
that are not supersingular are said to be ordinary.
The group  of points of an elliptic curve
of points of an elliptic curve 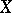 with orders that divide
with orders that divide  has the following structure:
has the following structure: 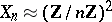 when
when 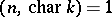 . For
. For  and ordinary elliptic curves
and ordinary elliptic curves 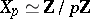 , while for supersingular elliptic curves
, while for supersingular elliptic curves  . For a prime number
. For a prime number  the Tate module
the Tate module 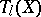 is isomorphic to
is isomorphic to  .
.
Elliptic curves over non-closed fields.
Let 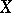 be an elliptic curve over an arbitrary field
be an elliptic curve over an arbitrary field 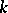 . If the set of
. If the set of 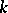 -rational points
-rational points 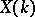 of
of 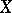 is not empty, then
is not empty, then 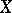 is biregularly isomorphic to a plane cubic curve (1) with
is biregularly isomorphic to a plane cubic curve (1) with  (
(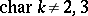 ). The point at infinity
). The point at infinity  of (1) is defined over
of (1) is defined over 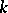 . As above, one can introduce a group structure on (1), turning
. As above, one can introduce a group structure on (1), turning 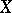 into a one-dimensional Abelian variety over
into a one-dimensional Abelian variety over 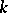 and turning the set
and turning the set 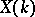 into an Abelian group with
into an Abelian group with 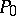 as trivial element. If
as trivial element. If  is finitely generated over its prime subfield, then
is finitely generated over its prime subfield, then 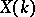 is a finitely-generated group (the Mordell–Weil theorem).
is a finitely-generated group (the Mordell–Weil theorem).
For any elliptic curve  there is defined the Jacobi variety
there is defined the Jacobi variety 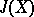 , which is a one-dimensional Abelian variety over
, which is a one-dimensional Abelian variety over 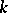 , and
, and  is a principal homogeneous space over
is a principal homogeneous space over  . If
. If 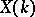 is not empty, then the choice of
is not empty, then the choice of 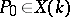 specifies an isomorphism
specifies an isomorphism 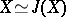 under which
under which  becomes the trivial element of
becomes the trivial element of  . In general,
. In general,  and
and 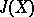 are isomorphic over a finite extension of
are isomorphic over a finite extension of 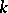 (see [1], [4], [13]).
(see [1], [4], [13]).
Elliptic curves over the field of complex numbers.
An elliptic curve over 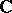 is a compact Riemann surface of genus 1, and vice versa. The group structure turns
is a compact Riemann surface of genus 1, and vice versa. The group structure turns 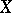 into a complex Lie group, which is a one-dimensional complex torus
into a complex Lie group, which is a one-dimensional complex torus 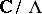 , where
, where 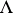 is a lattice in the complex plane
is a lattice in the complex plane  . Conversely, any one-dimensional complex torus is an elliptic curve (see [3]). From the topological point of view, an elliptic curve is a two-dimensional torus.
. Conversely, any one-dimensional complex torus is an elliptic curve (see [3]). From the topological point of view, an elliptic curve is a two-dimensional torus.
The theory of elliptic curves over 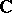 is in essence equivalent to the theory of elliptic functions. An identification of a torus
is in essence equivalent to the theory of elliptic functions. An identification of a torus 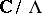 with an elliptic curve can be effected as follows. The elliptic functions with a given period lattice
with an elliptic curve can be effected as follows. The elliptic functions with a given period lattice 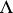 form a field generated by the Weierstrass
form a field generated by the Weierstrass 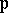 -function (see Weierstrass elliptic functions) and its derivative
-function (see Weierstrass elliptic functions) and its derivative 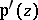 , which are connected by the relation
, which are connected by the relation
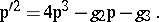 |
The mapping 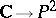 (
(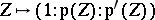 ) induces an isomorphism between the torus
) induces an isomorphism between the torus 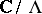 and the elliptic curve
and the elliptic curve 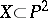 with equation
with equation  . The identification of
. The identification of 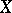 given by (1) with the torus
given by (1) with the torus 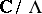 is effected by curvilinear integrals of the holomorphic form
is effected by curvilinear integrals of the holomorphic form 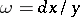 and gives an isomorphism
and gives an isomorphism 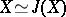 .
.
The description of the set of all elliptic curves as tori 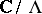 leads to the modular function
leads to the modular function 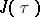 . Two lattices
. Two lattices 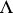 and
and 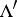 determine isomorphic tori if and only if they are similar, that is, if one is obtained from the other by multiplication by a complex number. Therefore it may be assumed that
determine isomorphic tori if and only if they are similar, that is, if one is obtained from the other by multiplication by a complex number. Therefore it may be assumed that 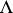 is generated by the numbers 1 and
is generated by the numbers 1 and  in
in 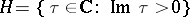 . Two lattices with bases
. Two lattices with bases  and
and 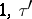 are similar if and only if
are similar if and only if 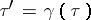 for an element
for an element 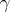 of the modular group
of the modular group 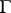 . The modular function
. The modular function
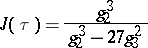 |
is also called the absolute invariant; 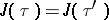 if and only if
if and only if  for some
for some 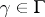 , and the function
, and the function 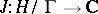 produces a one-to-one correspondence between the classes of isomorphic elliptic curves over
produces a one-to-one correspondence between the classes of isomorphic elliptic curves over 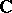 and the complex numbers. If
and the complex numbers. If 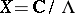 , then
, then  .
.
An elliptic curve 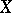 has complex multiplication if and only if
has complex multiplication if and only if  is an imaginary quadratic irrationality. In this case
is an imaginary quadratic irrationality. In this case 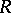 is a subring of finite index in the ring of algebraic integers of the imaginary quadratic field
is a subring of finite index in the ring of algebraic integers of the imaginary quadratic field 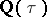 . Elliptic curves with complex multiplication are closely connected with the class field theory for imaginary quadratic fields (see [4], [8]).
. Elliptic curves with complex multiplication are closely connected with the class field theory for imaginary quadratic fields (see [4], [8]).
Arithmetic of elliptic curves.
Let  be an elliptic curve over the finite field
be an elliptic curve over the finite field 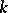 with
with 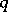 elements. The set
elements. The set 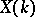 is always non-empty and finite. Hence
is always non-empty and finite. Hence 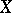 is endowed with the structure of a one-dimensional Abelian variety over
is endowed with the structure of a one-dimensional Abelian variety over 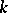 , and
, and 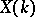 with that of a finite Abelian group. The order
with that of a finite Abelian group. The order 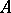 of
of  satisfies
satisfies 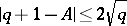 . The characteristic polynomial of the Frobenius endomorphism acting on the Tate module
. The characteristic polynomial of the Frobenius endomorphism acting on the Tate module  ,
,  , is
, is  . Its roots
. Its roots 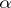 and
and  are complex-conjugate algebraic integers of modulus
are complex-conjugate algebraic integers of modulus 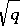 . For any finite extension
. For any finite extension 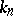 of
of 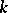 of degree
of degree  , the order of
, the order of  is
is 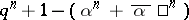 . The zeta-function of
. The zeta-function of  is
is
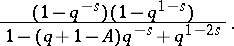 |
For any algebraic integer 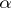 of modulus
of modulus 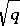 in some imaginary quadratic field (or in
in some imaginary quadratic field (or in  ) one can find an elliptic curve
) one can find an elliptic curve  over
over 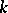 such that the order of
such that the order of  is
is  .
.
Let  be the field
be the field 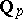 of
of 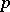 -adic numbers or a finite algebraic extension of it, let
-adic numbers or a finite algebraic extension of it, let 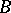 be the ring of integers of
be the ring of integers of 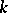 , let
, let 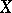 be an elliptic curve over
be an elliptic curve over 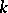 , and suppose that
, and suppose that 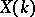 is non-empty. The group structure turns
is non-empty. The group structure turns 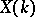 into a commutative compact one-dimensional
into a commutative compact one-dimensional  -adic Lie group (cf. Lie group,
-adic Lie group (cf. Lie group,  -adic). The group
-adic). The group  is Pontryagin-dual to the Weil–Châtelet group
is Pontryagin-dual to the Weil–Châtelet group 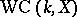 . If
. If  , then
, then  is a Tate curve (see [1], [5]) and there exists a canonical uniformization of
is a Tate curve (see [1], [5]) and there exists a canonical uniformization of 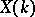 analogous to the case of
analogous to the case of  .
.
Let 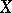 be an elliptic curve over
be an elliptic curve over 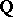 for which
for which  is not empty. Then
is not empty. Then  is biregularly isomorphic to the curve (1) with
is biregularly isomorphic to the curve (1) with 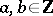 . Of all curves of the form (1) that are isomorphic to
. Of all curves of the form (1) that are isomorphic to 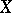 with integers
with integers  and
and  , one chooses the one for which the absolute value of the discriminant
, one chooses the one for which the absolute value of the discriminant  is minimal. The conductor
is minimal. The conductor 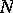 and the
and the 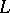 -function
-function 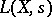 of
of  are defined as formal products of local factors:
are defined as formal products of local factors:
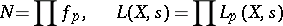 | (2) |
over all prime numbers 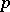 (see [1], [5], [13]). Here
(see [1], [5], [13]). Here 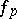 is some power of
is some power of 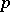 , and
, and  is a meromorphic function of the complex variable
is a meromorphic function of the complex variable  that has neither a zero nor a pole at
that has neither a zero nor a pole at 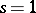 . To determine the local factors one considers the reduction of
. To determine the local factors one considers the reduction of  modulo
modulo 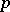 (
( ), which is a plane projective curve
), which is a plane projective curve 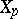 over the residue class field
over the residue class field 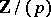 and is given in an affine coordinate system by the equation
and is given in an affine coordinate system by the equation
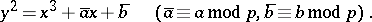 |
Let 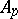 be the number of
be the number of  -points on
-points on  . If
. If 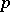 does not divide
does not divide  , then
, then 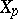 is an elliptic curve over
is an elliptic curve over 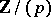 , and one puts
, and one puts
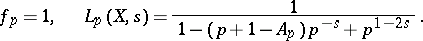 |
If  divides
divides 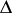 , then the polynomial
, then the polynomial 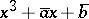 has a multiple root, and one puts
has a multiple root, and one puts
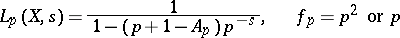 |
(depending on whether it is a triple or a double root). The product (2) converges in the right half-plane 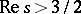 . It has been conjectured that
. It has been conjectured that 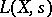 has a meromorphic extension to the whole complex plane and that the function
has a meromorphic extension to the whole complex plane and that the function
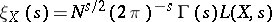 |
(where 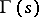 is the gamma-function) satisfies the functional equation
is the gamma-function) satisfies the functional equation  with
with 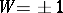 (see [5], [3]). This conjecture has been proved for elliptic curves with complex multiplication.
(see [5], [3]). This conjecture has been proved for elliptic curves with complex multiplication.
The group 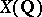 is isomorphic to
is isomorphic to 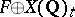 , where
, where  is a finite Abelian group and
is a finite Abelian group and 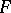 is a free Abelian group of a certain finite rank
is a free Abelian group of a certain finite rank  .
. 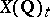 is isomorphic to one of the following 15 groups (see [11]):
is isomorphic to one of the following 15 groups (see [11]): 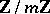 ,
,  or
or 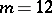 , and
, and  ,
, 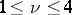 . The number
. The number  is called the rank of the elliptic curve over
is called the rank of the elliptic curve over 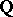 , or its
, or its 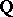 -rank. Examples are known of elliptic curves over
-rank. Examples are known of elliptic curves over  of rank
of rank 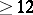 . There is a conjecture (see [1], [13]) that over
. There is a conjecture (see [1], [13]) that over 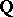 there exist elliptic curves of arbitrary large rank.
there exist elliptic curves of arbitrary large rank.
In the study of 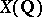 one uses the Tate height
one uses the Tate height 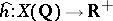 , which is a non-negative definite quadratic form on
, which is a non-negative definite quadratic form on 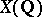 (see [1], [3], [8], and also Height, in Diophantine geometry). For any
(see [1], [3], [8], and also Height, in Diophantine geometry). For any  the set
the set 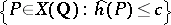 is finite. In particular,
is finite. In particular, 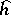 vanishes precisely on the torsion subgroup of
vanishes precisely on the torsion subgroup of  .
.
An important invariant of an elliptic curve is its Tate–Shafarevich group 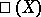 (see Weil–Châtelet group). The non-trivial elements of
(see Weil–Châtelet group). The non-trivial elements of 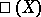 , an elliptic curve without
, an elliptic curve without  -points, provide examples of elliptic curves for which the Hasse principle fails to hold. The group
-points, provide examples of elliptic curves for which the Hasse principle fails to hold. The group 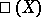 is periodic and for every
is periodic and for every  the subgroup of its elements of order dividing
the subgroup of its elements of order dividing  is finite. For a large number of elliptic curves it has been verified that the 2- and
is finite. For a large number of elliptic curves it has been verified that the 2- and  -components of
-components of  are finite (see [1], [4], [5]). There is a conjecture that
are finite (see [1], [4], [5]). There is a conjecture that  is finite.
is finite.
A conjecture of Birch and Swinnerton-Dyer asserts (see [5], [13]) that the order of the zero of the 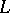 -function
-function  at
at 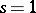 is equal to the
is equal to the  -rank of
-rank of 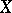 . In particular,
. In particular,  has a zero at
has a zero at 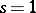 if and only if
if and only if 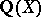 is infinite. So far (1984) the conjecture has not been proved for a single elliptic curve, but for elliptic curves with complex multiplication (and
is infinite. So far (1984) the conjecture has not been proved for a single elliptic curve, but for elliptic curves with complex multiplication (and  ) it has been established that when
) it has been established that when 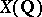 is infinite, then the
is infinite, then the 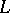 -function has a zero at
-function has a zero at 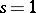 (see [14]). The conjecture of Birch and Swinnerton-Dyer gives the principal term of the asymptotic expansion of the
(see [14]). The conjecture of Birch and Swinnerton-Dyer gives the principal term of the asymptotic expansion of the 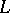 -function as
-function as 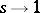 ; in it there occur the orders of the groups
; in it there occur the orders of the groups 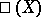 and
and 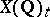 and the determinant of the Tate height [1]. It can be restated in terms of the Tamagawa numbers (cf. Tamagawa number, see [7]).
and the determinant of the Tate height [1]. It can be restated in terms of the Tamagawa numbers (cf. Tamagawa number, see [7]).
There is a conjecture of Weil that an elliptic curve  has a uniformization by modular functions relative to the congruence subgroup
has a uniformization by modular functions relative to the congruence subgroup  of the modular group
of the modular group  (see [5] and also Zeta-function in algebraic geometry). This conjecture has been proved for elliptic functions with complex multiplication. It is known (see [15]) that every algebraic curve over
(see [5] and also Zeta-function in algebraic geometry). This conjecture has been proved for elliptic functions with complex multiplication. It is known (see [15]) that every algebraic curve over  can be uniformized (cf. Uniformization) by modular functions relative to some subgroup of
can be uniformized (cf. Uniformization) by modular functions relative to some subgroup of 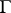 of finite index.
of finite index.
References
| [1] | J.W.S. Cassels, "Diophantine equations with special reference to elliptic curves" J. London Math. Soc. , 41 (1966) pp. 193–291 |
| [2] | A. Hurwitz, R. Courant, "Vorlesungen über allgemeine Funktionentheorie und elliptische Funktionen" , Springer (1968) |
| [3] | D. Mumford, "Abelian varieties" , Oxford Univ. Press (1974) |
| [4] | J.W.S. Cassels (ed.) A. Fröhlich (ed.) , Algebraic number theory , Acad. Press (1967) |
| [5] | Yu.I. Manin, "Cyclotomic fields and modular curves" Russian Math. Surveys , 26 : 6 (1971) pp. 6–78 Uspekhi Mat. Nauk , 26 : 6 (1971) pp. 7–71 |
| [6] | R. Hartshorne, "Algebraic geometry" , Springer (1977) pp. 91 |
| [7] | S. Bloch, "A note on height pairings, Tamagawa numbers, and the Birch and Swinnnerton-Dyer conjecture" Invent. Math. , 58 (1980) pp. 65–76 |
| [8] | S. Lang, "Elliptic curves; Diophantine analysis" , Springer (1978) |
| [9] | S. Lang, "Elliptic functions" , Addison-Wesley (1973) |
| [10] | B. Mazur, "Rational isogenies of prime degree" Invent. Math. , 44 (1978) pp. 129–162 |
| [11] | J.-P. Serre (ed.) P. Deligne (ed.) W. Kuyk (ed.) , Modular functions of one variable. 4 , Lect. notes in math. , 476 , Springer (1975) |
| [12] | J.F. Mestre, "Construction d'une courbe elliptique de rang 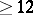 " C.R. Acad. Sci. Paris Sér. 1 , 295 (1982) pp. 643–644 " C.R. Acad. Sci. Paris Sér. 1 , 295 (1982) pp. 643–644 |
| [13] | J. Tate, "The arithmetic of elliptic curves" Invent. Math. , 23 (1974) pp. 197–206 |
| [14] | J. Coates, A. Wiles, "On the conjecture of Birch and Swinnerton-Dyer" Invent. Math. , 39 (1977) pp. 223–251 |
| [15] | G.V. Belyi, "On Galois extensions of a maximal cyclotomic field" Math. USSR Izv. , 14 : 2 (1980) pp. 247–256 Izv. Akad. Nauk SSSR Ser. Mat. , 43 (1979) pp. 267–276 |
Comments
References
| [a1] | B. Mazur, "Modular curves and the Eisenstein ideal" Publ. Math. IHES , 47 (1978) pp. 33–186 |
| [a2] | J.H. Silverman, "The arithmetic of elliptic curves" , Springer (1986) |
Elliptic curve. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Elliptic_curve&oldid=16112