Elimination of quantifiers
An elementary theory 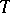 is said to admit elimination of quantifiers if every formula in
is said to admit elimination of quantifiers if every formula in 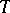 is equivalent in the language of
is equivalent in the language of 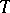 to a formula without quantifiers (having the same free variables). This holds if and only if
to a formula without quantifiers (having the same free variables). This holds if and only if 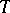 is substructure complete, i.e., for every two models
is substructure complete, i.e., for every two models 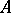 and
and 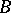 of
of 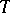 with a common substructure
with a common substructure 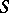 , the expansions
, the expansions 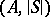 and
and 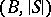 are elementarily equivalent in the first-order language of signature
are elementarily equivalent in the first-order language of signature 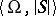 , where
, where  denotes the signature of
denotes the signature of 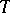 (cf. Model theory; Structure). If
(cf. Model theory; Structure). If 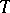 is substructure complete, then it is model complete. To see this, set
is substructure complete, then it is model complete. To see this, set 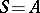 for every model
for every model 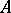 of
of 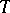 which is a substructure of a model
which is a substructure of a model  of
of  .
.
For certain elementary theories of fields, the fact that they admit elimination of quantifiers reflects an algebraic elimination theory. Examples are the theory of algebraically closed fields (where vanishing of the resultant, 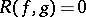 , gives a quantifier-free criterion for the existence of a common zero of two polynomials
, gives a quantifier-free criterion for the existence of a common zero of two polynomials 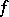 ,
, 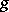 ), and the theory of real closed fields (where the Sturm theorem gives a quantifier-free criterion for a polynomial to admit a root in a given interval, cf. also Real closed field).
), and the theory of real closed fields (where the Sturm theorem gives a quantifier-free criterion for a polynomial to admit a root in a given interval, cf. also Real closed field).
The fact that the theory of real closed fields admits elimination of quantifiers is commonly known as the Tarski–Seidenberg theorem (see also Semi-algebraic set). It implies that the semi-algebraic sets over a real closed field 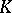 are precisely the definable sets (with parameters from
are precisely the definable sets (with parameters from 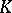 ) in the first-order language of ordered fields. For the history and applications of the Tarski–Seidenberg theorem, and a remarkable discussion of the general technique of elimination of quantifiers, see [a2] and the literature cited therein. For applications of elimination of quantifiers to real and
) in the first-order language of ordered fields. For the history and applications of the Tarski–Seidenberg theorem, and a remarkable discussion of the general technique of elimination of quantifiers, see [a2] and the literature cited therein. For applications of elimination of quantifiers to real and  -adic semi- and subanalytic sets, see [a1].
-adic semi- and subanalytic sets, see [a1].
For certain elementary theories of algebraic systems, elimination of quantifiers implies closure properties of their models (cf. [a3]).
References
| [a1] | J. Denef, L. van den Dries, "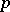 -adic and real subanalytic sets" Ann. of Math. , 128 (1988) pp. 79–138 -adic and real subanalytic sets" Ann. of Math. , 128 (1988) pp. 79–138 |
| [a2] | L. van den Dries, "Alfred Tarski's elimination theory for real closed fields" J. Symb. Logic , 53 (1988) pp. 7–19 |
| [a3] | L. van den Dries, A. Macintyre, K. McKenna, "Elimination of quantifiers in algebraic structures" Adv. in Math. , 47 (1983) pp. 74–87 |
Elimination of quantifiers. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Elimination_of_quantifiers&oldid=17833