Elementary flow
A random sequence of moments of time  at which the events of a flow of events take place (e.g. a flow of incoming calls at a telephone station), and for which the differences
at which the events of a flow of events take place (e.g. a flow of incoming calls at a telephone station), and for which the differences  satisfy the condition of independence and have the same exponential distribution. An elementary flow with distribution
satisfy the condition of independence and have the same exponential distribution. An elementary flow with distribution
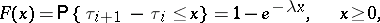 | (*) |
is a particular case of a renewal process (cf. Renewal theory). To an elementary flow is related the Poisson process 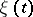 equal to the number of events of the flow in the time interval
equal to the number of events of the flow in the time interval  . An elementary flow and its related Poisson process satisfy the following conditions.
. An elementary flow and its related Poisson process satisfy the following conditions.
Stationarity. For any  ,
,  the distribution of the random variable
the distribution of the random variable
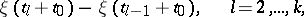 |
does not depend on  .
.
Orderliness. The probability of occurrence of two or more events of the flow in the interval  is equal to
is equal to 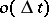 as
as 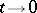 .
.
Lack of memory. For  the random variables
the random variables 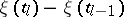 ,
, 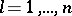 , are independent.
, are independent.
It turns out that in these circumstances and under the condition
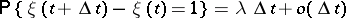 |
the flow is elementary with exponential distribution (*).
References
| [1] | A.Ya. Khinchin, "Mathematical methods in the theory of queueing" , Griffin (1960) (Translated from Russian) |
Elementary flow. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Elementary_flow&oldid=18634