Effective Nullstellensatz
Let  , where
, where  is a field. Hilbert's Nullstellensatz [a5] says that if
is a field. Hilbert's Nullstellensatz [a5] says that if  vanishes on all the common zeros of the
vanishes on all the common zeros of the  with coordinates in an algebraic closure of
with coordinates in an algebraic closure of  , then, for some integer
, then, for some integer  ,
,  , i.e. there exist
, i.e. there exist  such that
such that
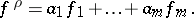 |
An effective Nullstellensatz gives information on some aspect of the complexity of such a representation.
Degree bounds.
If 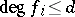 , how large might one have to take
, how large might one have to take 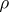 and
and 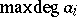 ?
?
The projective version of the Masser–Philippon/Lazard–Mora example shows that this bound must be at least 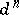 . Although classical work of G. Hermann [a8] produces an explicit bound [a14], it is known that
. Although classical work of G. Hermann [a8] produces an explicit bound [a14], it is known that 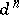 is the correct one [a16], [a17], [a11].
is the correct one [a16], [a17], [a11].
Height bounds.
How large might a common denominator or the numerators of the 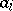 be?
be?
Assume, in addition, that 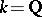 and that when the coefficients of all the
and that when the coefficients of all the 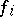 are put over a common denominator, the absolute values of that denominator and the numerators of the coefficients are at most
are put over a common denominator, the absolute values of that denominator and the numerators of the coefficients are at most 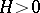 . One can, of course, first bound the degrees, and then apply estimates from linear algebra to obtain a bound of the unfortunate shape
. One can, of course, first bound the degrees, and then apply estimates from linear algebra to obtain a bound of the unfortunate shape 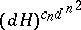 . In fact, by [a15], a denominator of absolute value at most
. In fact, by [a15], a denominator of absolute value at most 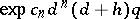 suffices, with explicit
suffices, with explicit 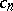 . The same is true of the numerators if one allows slightly larger than optimal bounds on the degrees of the
. The same is true of the numerators if one allows slightly larger than optimal bounds on the degrees of the 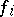 :
: 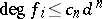 [a2], [a3], [a13].
[a2], [a3], [a13].
Complexity bounds.
In the various models of computation, how many steps might be involved in finding such a representation?
In these models, as in the above classical case for heights, the complexity bounds turn out to be better than that obtained by simply applying linear algebra and using the degree bounds. Many interesting aspects, such as sparsity of the coefficients, arise. See [a9] for an introduction to a sizable and growing literature.
Generalizations.
Various effective generalizations of Hilbert's Nullstellensatz exist, cf. [a19], [a6], [a12], as well as insight into important special situations [a10]. See [a1] for the link between the complexity of the Nullstellensatz and the problem 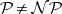 (cf.
(cf. 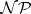 ).
).
References
| [a1] | L. Blum, F. Cuker, M. Schub, S. Smale, "Complexity and real computation" , Springer (1998) |
| [a2] | C.A. Berenstein, A. Yger, "Effective Bezout identities in 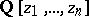 " Acta Math. , 166 (1991) pp. 69–120 " Acta Math. , 166 (1991) pp. 69–120 |
| [a3] | C.A. Berenstein, A. Yger, "Residue calculus and effective Nullstellensatz" Amer. J. Math. , 121 (1999) pp. 723–796 |
| [a4] | L. Caniglia, A. Galligo, J. Heintz, "Borne simplement exponentielle pour les degrés dans le théorème des zéros sur un corps de characteristique quelconque" C.R. Acad. Sci. Paris , 307 (1988) pp. 255–258 |
| [a5] | D. Hilbert, "Über die vollen Invariantesysteme" Math. Ann. , 42 (1893) pp. 313–373 (Also: Ges. Abh., II, pp. 287-344) |
| [a6] | L. Ein, R. Lazarsfeld, "A geometric effective Nullstellensatz" Invent. Math. , 137 (1999) pp. 427–448 |
| [a7] | N. Fitchas, A. Galligo, "Nullstellensatz effectif et conjecture de Serre (théorème de Quillen–Suslin) pour le calcul formel" Math. Nachr. , 149 (1990) pp. 231–253 |
| [a8] | G. Hermann, "Die Frage der endlich vielen Schritte in der Theorie der Polynomideale" Math. Ann. , 95 (1926) pp. 736–788 |
| [a9] | M. Giusti, J. Heintz, J.E. Morais, J. Morgenstern, L.M. Pardo, "Straight-line programs in geometric elimination theory" J. Pure Appl. Algebra , 124 (1998) pp. 101–146 |
| [a10] | I. Ojeda, R. Piedra, "Effective Nullstellensatz for binomial ideals" Manuscript (2000) |
| [a11] | J. Kollár, "Sharp effective Nullstellensatz" J. Amer. Math. Soc. , 1 (1988) pp. 963–975 |
| [a12] | J. Kollár, "Effective Nullstellensatz for arbitrary ideals" J. Europ. Math. Soc. (JEMS) , 1 (1999) pp. 313–337 |
| [a13] | T. Krick, L.M. Pardo, M. Sombra, "Sharp estimates for the arithmetic Nullstellensatz" http://front.math.ucdavis.edu , math.AG/9911094 (1999) |
| [a14] | D.W. Masser, G. Wüsholz, "Fields of large transcendence degree generated by values of elliptic functions" Invent. Math. , 72 (1983) pp. 407–464 |
| [a15] | P. Phillipon, "Dénominateurs dans le théorème des zéros de Hilbert" Acta Arith. , 58 (1990) pp. 1–25 |
| [a16] | W.D. Brownawell, "Bounds for the degrees in the Nullstellensatz" Ann. of Math. , 126 (1987) pp. 577–591 |
| [a17] | W.D. Brownawell, "Borne effective pour l'exposant dans le théorème des zéros" C.R. Acad. Sci. Paris , 305 (1987) pp. 287–290 |
| [a18] | W.D. Brownawell, "Local diophantine Nullstellen equalities" J. Amer. Math. Soc. , 1 (1988) pp. 311–322 |
| [a19] | W.D. Brownawell, "A pure power product version of the Hilbert Nullstellensatz" Michigan Math. J. , 45 (1998) pp. 581–597 |
Effective Nullstellensatz. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Effective_Nullstellensatz&oldid=16412