Duality in complex analysis
Let 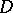 be a domain in
be a domain in 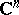 and denote by
and denote by 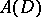 the space of all functions holomorphic in
the space of all functions holomorphic in 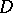 with the topology of uniform convergence on compact subsets of
with the topology of uniform convergence on compact subsets of  (the projective limit topology). Let
(the projective limit topology). Let 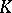 be a compact set in
be a compact set in  . Similarly, let
. Similarly, let 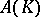 be the space of all functions holomorphic on
be the space of all functions holomorphic on 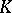 endowed with the following topology: A sequence
endowed with the following topology: A sequence 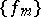 converges to a function
converges to a function 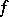 in
in 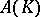 if there exists a neighbourhood
if there exists a neighbourhood  such that all the functions
such that all the functions 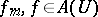 and
and 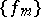 converges to
converges to 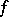 in
in  (the inductive limit topology).
(the inductive limit topology).
The description of the dual spaces 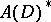 and
and 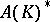 is one of the main problems in the concrete functional analysis of spaces of holomorphic functions.
is one of the main problems in the concrete functional analysis of spaces of holomorphic functions.
Grothendieck–Köthe–Sebastião e Silva duality.
Let 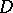 be a domain in the complex plane
be a domain in the complex plane 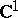 and let
and let
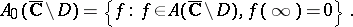 |
Then one has the isomorphism (see [a1], [a2], [a3])
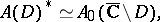 |
defined by
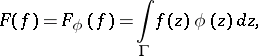 | (a1) |
where 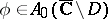 . Here,
. Here, 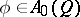 , where
, where 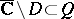 for some domain
for some domain 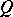 ; and the curve
; and the curve 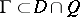 separates the singularities of the functions
separates the singularities of the functions 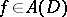 and
and 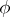 . The integral in (a1) does not depend on the choice of
. The integral in (a1) does not depend on the choice of 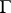 .
.
Duality and linear convexity.
When 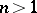 , the complement of a bounded domain
, the complement of a bounded domain 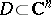 is not useful for function theory. Indeed, if
is not useful for function theory. Indeed, if 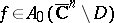 , then
, then 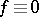 . However, a generalized notion of "exterior" does exist for linearly convex domains and compacta.
. However, a generalized notion of "exterior" does exist for linearly convex domains and compacta.
A domain 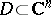 is called linearly convex if for any
is called linearly convex if for any 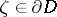 there exists a complex hyperplane
there exists a complex hyperplane 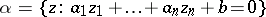 through
through 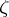 that does not intersect
that does not intersect 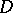 . A compact set
. A compact set 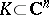 is called linearly convex if it can be approximated from the outside by linearly convex domains. Observe that the topological dimension of
is called linearly convex if it can be approximated from the outside by linearly convex domains. Observe that the topological dimension of 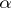 is
is 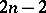 .
.
Some examples:
1) Let 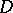 be convex; then for any point
be convex; then for any point 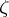 of the boundary
of the boundary 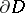 there exists a hyperplane of support
there exists a hyperplane of support 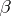 of dimension
of dimension 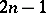 that contains the complex hyperplane
that contains the complex hyperplane 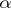 .
.
2) Let 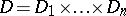 , where
, where 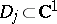 ,
, 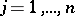 , are arbitrary plane domains.
, are arbitrary plane domains.
Let 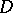 be approximated from within by the sequence of linearly convex domains
be approximated from within by the sequence of linearly convex domains  with smooth boundaries:
with smooth boundaries: 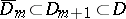 , where
, where 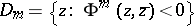 ,
, 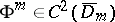 , and
, and 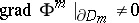 . Such an approximation does not always exist, unlike the case of usual convexity. For instance, this approximation is impossible in Example 2) if at least one of the domains
. Such an approximation does not always exist, unlike the case of usual convexity. For instance, this approximation is impossible in Example 2) if at least one of the domains 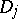 is non-convex.
is non-convex.
If 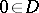 , one has the isomorphism
, one has the isomorphism
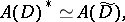 |
where 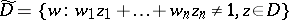 is the adjoint set (the generalized complement) defined by
is the adjoint set (the generalized complement) defined by
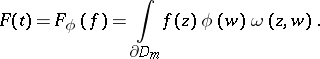 | (a2) |
Here, 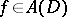 ,
, 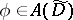 ,
,
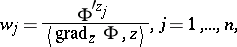 |
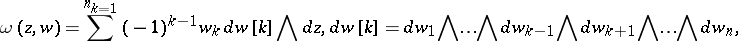 |
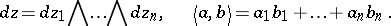 |
The index  depends on the function
depends on the function 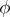 , which is holomorphic on the larger compact set
, which is holomorphic on the larger compact set 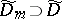 . The integral in (a4) does not depend on the choice of
. The integral in (a4) does not depend on the choice of  .
.
A similar duality is valid for the space 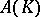 as well (see [a4], [a5], [a6]).
as well (see [a4], [a5], [a6]).
A. Martineau has defined a strongly linearly convex domain 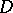 to be a linearly convex domain for which the above-mentioned isomorphism holds. It is proved in [a7] that a domain
to be a linearly convex domain for which the above-mentioned isomorphism holds. It is proved in [a7] that a domain 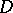 is strongly linearly convex if and only if the intersection of
is strongly linearly convex if and only if the intersection of 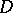 with any complex line is connected and simply connected (see also [a8], [a9], [a10], [a11]).
with any complex line is connected and simply connected (see also [a8], [a9], [a10], [a11]).
Duality based on regularized integration over the boundary.
L. Stout obtained the following result for bounded domains 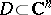 with the property that, for a fixed
with the property that, for a fixed 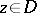 , the Szegö kernel
, the Szegö kernel 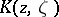 is real-analytic in
is real-analytic in 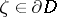 . Apparently, this is true if
. Apparently, this is true if 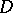 is a strictly pseudo-convex domain with real-analytic boundary. Then the isomorphism
is a strictly pseudo-convex domain with real-analytic boundary. Then the isomorphism
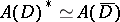 | (a3) |
is defined by the formula
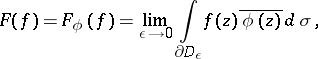 |
Nacinovich–Shlapunov–Tarkhanov theorem.
Let 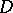 be a bounded domain in
be a bounded domain in 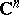 with real-analytic boundary and with the property that any neighbourhood
with real-analytic boundary and with the property that any neighbourhood 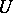 of
of  contains a neighbourhood
contains a neighbourhood 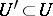 such that
such that 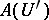 is dense in
is dense in 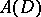 . This is always the case if
. This is always the case if 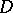 is a strictly pseudo-convex domain with real-analytic boundary.
is a strictly pseudo-convex domain with real-analytic boundary.
For any function 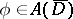 there exists a unique solution of the Dirichlet problem
there exists a unique solution of the Dirichlet problem
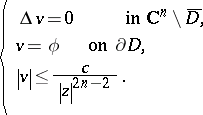 |
Here, the isomorphism (a3) can be defined by the formula (see [a14])
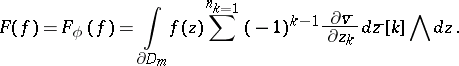 | (a4) |
The integral is well-defined for some  (where
(where 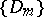 is a sequence of domains with smooth boundaries which approximate
is a sequence of domains with smooth boundaries which approximate 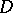 from within) since the function
from within) since the function  , which is harmonic in
, which is harmonic in 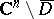 , can be harmonically continued into
, can be harmonically continued into  for some
for some 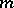 because of the real analyticity of
because of the real analyticity of 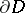 and
and 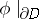 . The integral in (a4) does not depend on the choice of
. The integral in (a4) does not depend on the choice of 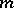 .
.
Duality and cohomology.
Let 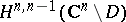 be the Dolbeault cohomology space
be the Dolbeault cohomology space
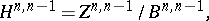 |
where 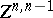 is the space of all
is the space of all 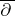 -closed forms
-closed forms 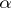 that are in
that are in 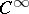 on some neighbourhood
on some neighbourhood 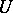 of
of 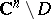 (the neighbourhood depends on the cocycle
(the neighbourhood depends on the cocycle 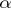 ) and
) and 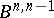 is the subspace of
is the subspace of 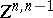 of all
of all 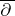 -exact forms
-exact forms 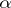 (coboundaries).
(coboundaries).
If 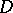 is a bounded pseudo-convex domain, then one has [a15], [a16] an isomorphism
is a bounded pseudo-convex domain, then one has [a15], [a16] an isomorphism
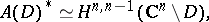 |
defined by the formula
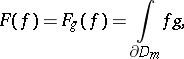 | (a5) |
where 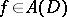 ,
, 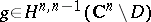 . Here, for some
. Here, for some 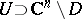 one has
one has 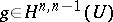 ;
; 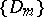 is a sequence of domains with smooth boundaries approximating
is a sequence of domains with smooth boundaries approximating 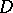 from within. Although
from within. Although 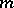 depends on the choice of
depends on the choice of 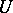 , the integral in (a5) does not depend on
, the integral in (a5) does not depend on 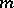 (given (a5), the same formula is valid for larger
(given (a5), the same formula is valid for larger  as well).
as well).
A new result [a17] consists of the following: Let 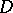 be a bounded pseudo-convex domain in
be a bounded pseudo-convex domain in 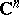 that can be approximated from within by a sequence of strictly pseudo-convex domains
that can be approximated from within by a sequence of strictly pseudo-convex domains 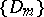 ; and let
; and let 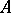 be the subspace of
be the subspace of 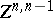 consisting of the differential forms of type
consisting of the differential forms of type
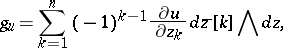 | (a6) |
where  is a function that is harmonic in some neighbourhood
is a function that is harmonic in some neighbourhood 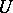 of
of  (which depends on
(which depends on  ) such that
) such that
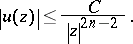 |
Let 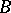 be the space of all forms of type (a6) such that the harmonic function
be the space of all forms of type (a6) such that the harmonic function 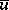 is representable for some
is representable for some 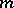 by the Bochner–Martinelli-type integral (cf. also Bochner–Martinelli representation formula)
by the Bochner–Martinelli-type integral (cf. also Bochner–Martinelli representation formula)
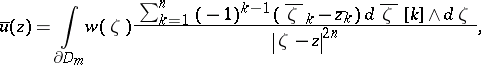 |
where 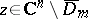 and
and 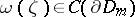 . Then one has an isomorphism
. Then one has an isomorphism
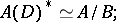 |
it is defined by the formula
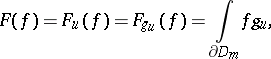 | (a7) |
where 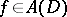 and
and 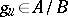 . Note that (a7) gives a more concrete description of the duality than does (a5). The integral in (a7) is also independent of the choice of
. Note that (a7) gives a more concrete description of the duality than does (a5). The integral in (a7) is also independent of the choice of 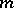 .
.
Other descriptions of the spaces dual to spaces of holomorphic functions for special classes of domains can be found in [a18], [a19], [a20], [a21], [a22], [a23], [a24], [a10].
References
| [a1] | A. Grothendieck, "Sur certain espaces de fonctions holomorphes" J. Reine Angew. Math. , 192 (1953) pp. 35–64; 77–95 |
| [a2] | G. Köthe, "Dualität in der Funktionentheorie" J. Reine Angew. Math. , 191 (1953) pp. 30–39 |
| [a3] | J. Sebastião e Silva, "Analytic functions in functional analysis" Portug. Math. , 9 (1950) pp. 1–130 |
| [a4] | A. Martineau, "Sur la topologies des espaces de fonctions holomorphes" Math. Ann. , 163 (1966) pp. 62–88 |
| [a5] | L. Aizenberg, "The general form of a linear continuous functional in spaces of functions holomorphic in convex domains in 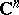 " Soviet Math. Dokl. , 7 (1966) pp. 198–202 " Soviet Math. Dokl. , 7 (1966) pp. 198–202 |
| [a6] | L. Aizenberg, "Linear convexity in 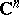 and the distributions of the singularities of holomorphic functions" Bull. Acad. Polon. Sci. Ser. Math. Astr. Phiz. , 15 (1967) pp. 487–495 (In Russian) and the distributions of the singularities of holomorphic functions" Bull. Acad. Polon. Sci. Ser. Math. Astr. Phiz. , 15 (1967) pp. 487–495 (In Russian) |
| [a7] | S.V. Zhamenskij, "A geometric criterion of strong linear convexity" Funct. Anal. Appl. , 13 (1979) pp. 224–225 |
| [a8] | M. Andersson, "Cauchy–Fantappié–Leray formulas with local sections and the inverse Fantappié transform" Bull. Soc. Math. France , 120 (1992) pp. 113–128 |
| [a9] | S.G. Gindikin, G.M. Henkin, "Integral geometry for  -cohomologies in -cohomologies in  -linearly concave domains in -linearly concave domains in  " Funct. Anal. Appl. , 12 (1978) pp. 6–23 " Funct. Anal. Appl. , 12 (1978) pp. 6–23 |
| [a10] | S.V. Znamenskij, "Strong linear convexity. I: Duality of spaces of holomorphic functions" Sib. Math. J. , 26 (1985) pp. 331–341 |
| [a11] | S.V. Znamenskij, "Strong linear convexity. II: Existence of holomorphic solutions of linear systems of equations" Sib. Math. J. , 29 (1988) pp. 911–925 |
| [a12] | L. Aizenberg, S.G. Gindikin, "The general form of a linear continuous functional in spaces of holomorphic functions" Moskov. Oblast. Ped. Just. Uchen. Zap. , 87 (1964) pp. 7–15 (In Russian) |
| [a13] | E.L. Stout, "Harmonic duality, hyperfunctions and removable singularities" Izv. Akad. Nauk Ser. Mat. , 59 (1995) pp. 133–170 |
| [a14] | M. Nacinovich, A. Shlapunov, N. Tarkhanov, "Duality in the spaces of solutions of elliptic systems" Ann. Scuola Norm. Sup. Pisa , 26 (1998) pp. 207–232 |
| [a15] | J.P. Serre, "Une théorème de dualité" Comment. Math. Helvetici , 29 (1955) pp. 9–26 |
| [a16] | A. Martineau, "Sur les fonctionelles analytiques et la transformation de Fourier–Borel" J. Anal. Math. , 9 (1963) pp. 1–164 |
| [a17] | L. Aizenberg, "Duality in complex analysis" , Israel Math. Conf. Proc. , 11 (1997) pp. 27–35 |
| [a18] | H.G. Tillman, "Randverteilungen analytischer funktionen und distributionen" Math. Z. , 59 (1953) pp. 61–83 |
| [a19] | S. Rolewicz, "On spaces of holomorphic function" Studia Math. , 21 (1962) pp. 135–160 |
| [a20] | L. Aizenberg, B.S. Mityagin, "The spaces of functions analytic in multi-circular domains" Sib. Mat. Zh. , 1 (1960) pp. 153–170 (In Russian) |
| [a21] | L. Aizenberg, "The spaces of functions analytic in  -circular domains" Soviet Math. Dokl. , 2 (1961) pp. 75–82 -circular domains" Soviet Math. Dokl. , 2 (1961) pp. 75–82 |
| [a22] | L.J. Ronkin, "On general form of functionals in space of functions, analytic in semicircular domain" Soviet Math. Dokl. , 2 (1961) pp. 673–686 |
| [a23] | S.G. Gindikin, "Analytic functions in tubular domains" Soviet Math. Dokl. , 3 (1962) |
| [a24] | S.D. Simonzhenkov, "Description of the conjugate space of functions that are holomorphic in the domain of a special type" Sib. Math. J. , 22 (1981) |
Duality in complex analysis. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Duality_in_complex_analysis&oldid=18633
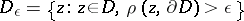 ,
, 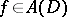 ,
, 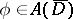 (see
(see