Drinfel'd-Turaev quantization
From Encyclopedia of Mathematics
A type of quantization typically encountered in knot theory, for example in Jones–Conway, homotopy or Kauffman bracket skein modules of three-dimensional manifolds ([a3], [a1], [a2], cf. also Skein module).
Fix a commutative ring with identity,  . Let
. Let  be a Poisson algebra over
be a Poisson algebra over  and let
and let  be an algebra over
be an algebra over  which is free as an
which is free as an  -module (cf. also Free module). An
-module (cf. also Free module). An  -module epimorphism
-module epimorphism  is called a Drinfel'd–Turaev quantization of
is called a Drinfel'd–Turaev quantization of  if
if
i) 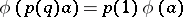 for all
for all  and all
and all  ; and
; and
ii)  for all
for all  .
.
If  is not required to be free as an
is not required to be free as an  -module, one obtains a so-called weak Drinfel'd–Turaev quantization.
-module, one obtains a so-called weak Drinfel'd–Turaev quantization.
References
| [a1] | J. Hoste, J.H. Przytycki, "Homotopy skein modules of oriented  -manifolds" Math. Proc. Cambridge Philos. Soc. , 108 (1990) pp. 475–488 -manifolds" Math. Proc. Cambridge Philos. Soc. , 108 (1990) pp. 475–488 |
| [a2] | J.H. Przytycki, "Homotopy and  -homotopy skein modules of -homotopy skein modules of  -manifolds: An example in Algebra Situs" , Proc. Conf. in Low-Dimensional Topology in Honor of Joan Birman's 70th Birthday (Columbia Univ./Barnard College, March, 14-15, 1998) , Internat. Press (2000) -manifolds: An example in Algebra Situs" , Proc. Conf. in Low-Dimensional Topology in Honor of Joan Birman's 70th Birthday (Columbia Univ./Barnard College, March, 14-15, 1998) , Internat. Press (2000) |
| [a3] | V.G. Turaev, "Skein quantization of Poisson algebras of loops on surfaces" Ann. Sci. École Norm. Sup. , 4 : 24 (1991) pp. 635–704 |
How to Cite This Entry:
Drinfel'd-Turaev quantization. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Drinfel%27d-Turaev_quantization&oldid=17078
Drinfel'd-Turaev quantization. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Drinfel%27d-Turaev_quantization&oldid=17078
This article was adapted from an original article by Jozef Przytycki (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article