Difference between revisions of "Divisorial ideal"
(Importing text file) |
m (link) |
||
| Line 1: | Line 1: | ||
| − | A [[Fractional ideal|fractional ideal]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033730/d0337301.png" /> of an integral commutative ring <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033730/d0337302.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033730/d0337303.png" /> (here <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033730/d0337304.png" /> denotes the set of elements <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033730/d0337305.png" /> of the field of fractions of the ring <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033730/d0337306.png" /> for which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033730/d0337307.png" />). A divisorial ideal is sometimes called a divisor of the ring. For any fractional ideal <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033730/d0337308.png" /> the ideal <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033730/d0337309.png" /> is divisorial. The set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033730/d03373010.png" /> of divisorial ideals of the ring <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033730/d03373011.png" /> is a lattice-ordered commutative monoid (semi-group) if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033730/d03373012.png" /> is considered to be the product of two divisorial ideals <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033730/d03373013.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033730/d03373014.png" />, while the integral divisorial ideals <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033730/d03373015.png" /> are considered as positive (or effective). The monoid <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033730/d03373016.png" /> is a group if and only if the ring <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033730/d03373017.png" /> is completely integrally closed; in that case, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033730/d03373018.png" /> is the inverse of the divisor <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033730/d03373019.png" />. | + | A [[Fractional ideal|fractional ideal]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033730/d0337301.png" /> of an integral commutative ring <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033730/d0337302.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033730/d0337303.png" /> (here <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033730/d0337304.png" /> denotes the set of elements <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033730/d0337305.png" /> of the [[field of fractions]] of the ring <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033730/d0337306.png" /> for which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033730/d0337307.png" />). A divisorial ideal is sometimes called a divisor of the ring. For any fractional ideal <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033730/d0337308.png" /> the ideal <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033730/d0337309.png" /> is divisorial. The set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033730/d03373010.png" /> of divisorial ideals of the ring <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033730/d03373011.png" /> is a lattice-ordered commutative monoid (semi-group) if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033730/d03373012.png" /> is considered to be the product of two divisorial ideals <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033730/d03373013.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033730/d03373014.png" />, while the integral divisorial ideals <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033730/d03373015.png" /> are considered as positive (or effective). The monoid <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033730/d03373016.png" /> is a group if and only if the ring <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033730/d03373017.png" /> is completely integrally closed; in that case, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033730/d03373018.png" /> is the inverse of the divisor <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033730/d03373019.png" />. |
Divisorial ideals are usually considered in a Krull ring (e.g. in a Noetherian integrally closed ring); here, prime ideals of height 1 are divisorial and form a basis of the Abelian group of divisors <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033730/d03373020.png" />. This result is in fact due to E. Artin and B.L. van der Waerden [[#References|[1]]], and forms part of their theory of quasi-equality of ideals (two ideals <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033730/d03373021.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033730/d03373022.png" /> are called quasi-equal if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033730/d03373023.png" />), which forms one of the principal subjects in algebra of these days — the study of factorization of ideals. | Divisorial ideals are usually considered in a Krull ring (e.g. in a Noetherian integrally closed ring); here, prime ideals of height 1 are divisorial and form a basis of the Abelian group of divisors <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033730/d03373020.png" />. This result is in fact due to E. Artin and B.L. van der Waerden [[#References|[1]]], and forms part of their theory of quasi-equality of ideals (two ideals <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033730/d03373021.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033730/d03373022.png" /> are called quasi-equal if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033730/d03373023.png" />), which forms one of the principal subjects in algebra of these days — the study of factorization of ideals. | ||
Revision as of 20:58, 28 November 2014
A fractional ideal  of an integral commutative ring
of an integral commutative ring 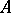 such that
such that 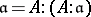 (here
(here 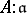 denotes the set of elements
denotes the set of elements  of the field of fractions of the ring
of the field of fractions of the ring  for which
for which 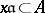 ). A divisorial ideal is sometimes called a divisor of the ring. For any fractional ideal
). A divisorial ideal is sometimes called a divisor of the ring. For any fractional ideal  the ideal
the ideal  is divisorial. The set
is divisorial. The set 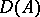 of divisorial ideals of the ring
of divisorial ideals of the ring 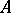 is a lattice-ordered commutative monoid (semi-group) if
is a lattice-ordered commutative monoid (semi-group) if 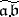 is considered to be the product of two divisorial ideals
is considered to be the product of two divisorial ideals  and
and 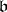 , while the integral divisorial ideals
, while the integral divisorial ideals 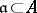 are considered as positive (or effective). The monoid
are considered as positive (or effective). The monoid 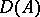 is a group if and only if the ring
is a group if and only if the ring 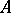 is completely integrally closed; in that case,
is completely integrally closed; in that case, 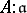 is the inverse of the divisor
is the inverse of the divisor  .
.
Divisorial ideals are usually considered in a Krull ring (e.g. in a Noetherian integrally closed ring); here, prime ideals of height 1 are divisorial and form a basis of the Abelian group of divisors 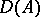 . This result is in fact due to E. Artin and B.L. van der Waerden [1], and forms part of their theory of quasi-equality of ideals (two ideals
. This result is in fact due to E. Artin and B.L. van der Waerden [1], and forms part of their theory of quasi-equality of ideals (two ideals  and
and 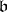 are called quasi-equal if
are called quasi-equal if  ), which forms one of the principal subjects in algebra of these days — the study of factorization of ideals.
), which forms one of the principal subjects in algebra of these days — the study of factorization of ideals.
Principal fractional ideals, as well as invertible fractional ideals, are divisorial and form subgroups 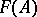 and
and 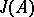 in
in 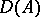 , respectively. The quotient groups
, respectively. The quotient groups 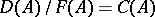 and
and  are known, respectively, as the divisor class group and the Picard group of
are known, respectively, as the divisor class group and the Picard group of 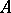 .
.
References
| [1] | B.L. van der Waerden, "Algebra" , 1–2 , Springer (1967–1971) (Translated from German) |
| [2] | N. Bourbaki, "Elements of mathematics. Commutative algebra" , Addison-Wesley (1972) (Translated from French) |
Divisorial ideal. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Divisorial_ideal&oldid=13538